阅读资料:
如图1,在平面之间坐标系xOy中,A,B两点的坐标分别为A(x1,y1),B(x2,y2),由勾股定理得AB2=|x2﹣x1|2+|y2﹣y1|2,所以A,B两点间的距离为AB= .
.
我们知道,圆可以看成到圆心距离等于半径的点的集合,如图2,在平面直角坐标系xoy中,A(x,y)为圆上任意一点,则A到原点的距离的平方为OA2=|x﹣0|2+|y﹣0|2,当⊙O的半径为r时,⊙O的方程可写为:x2+y2=r2.
问题拓展:如果圆心坐标为P(a,b),半径为r,那么⊙P的方程可以写为 .
综合应用:
如图3,⊙P与x轴相切于原点O,P点坐标为(0,6),A是⊙P上一点,连接OA,使tan∠POA= ,作PD⊥OA,垂足为D,延长PD交x轴于点B,连接AB.
,作PD⊥OA,垂足为D,延长PD交x轴于点B,连接AB.
①证明AB是⊙P的切点;
②是否存在到四点O,P,A,B距离都相等的点Q?若存在,求Q点坐标,并写出以Q为圆心,以OQ为半径的⊙O的方程;若不存在,说明理由.

如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.求证:BC∥EF.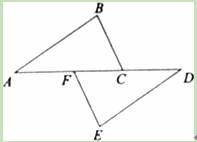
解不等式2x﹣3< ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.
某校宣传栏中公示了担任下学期七年级班主任的12位老师的情况(见下表),小凤准备到该校就读七年级,请根据表中信息帮小凤进行如下统计分析:
| 姓名 |
性别 |
年龄 |
学历 |
职称 |
姓名 |
性别 |
年龄 |
学历 |
职称 |
|
| 王雄辉 |
男 |
35 |
本科 |
高级 |
蔡波 |
男 |
45 |
大专 |
高级 |
|
| 李红 |
男 |
40 |
本科 |
中级 |
李凤 |
女 |
27 |
本科 |
初级 |
|
| 刘梅英 |
女 |
40 |
中专 |
中级 |
孙焰 |
男 |
40 |
大专 |
中级 |
|
| 张英 |
女 |
43 |
大专 |
高级 |
彭朝阳 |
男 |
30 |
大专 |
初级 |
|
| 刘元 |
男 |
50 |
中专 |
中级 |
龙妍 |
女 |
25 |
本科 |
初级 |
|
| 袁桂 |
男 |
30 |
本科 |
初级 |
杨书 |
男 |
40 |
本科 |
中级 |
(1)该校下学期七年级班主任老师年龄的众数是多少?
(2)在图7(1)中,将反映老师学历情况的条形统计图补充完整;
(3)在图7(2)中,标注扇形统计图中表示老师职称为初级和高级的百分比;
(4)小凤到该校就读七年级,班主任老师是女老师的概率是多少?

图10是小红设计的钻石形商标,△ABC是边长为2的等边三角形,四边形ACDE是等腰梯形,AC∥ED,∠EAC=60°,AE=1.
(1)证明:△ABE≌△CBD;
(2)图中存在多对相似三角形,请你找出一对进行证明,并求出其相似比(不添加辅助线,不找全等的相似三角形);
(3)小红发现AM=MN=NC,请证明此结论;
(4)求线段BD的长.
如图9,已知抛物线经过定点A(1,0),它的顶点P是y轴正半轴上的一个动点,P点关于x轴的对称点为P′,过P′ 作x轴的平行线交抛物线于B、D两点(B点在y轴右侧),直线BA交y轴于C点.按从特殊到一般的规律探究线段CA与CB的比值:
(1)当P点坐标为(0,1)时,写出抛物线的解析式并求线段CA与CB的比值;
(2)若P点坐标为(0,m)时(m为任意正实数),线段CA与CB的比值是否与⑴所求的比值相同?请说明理由.