如图,在直角坐标系中,Rt△OAB的直角顶点A在x轴上,OA=4,AB=3.动点M从点A出发,以每秒1个单位长度的速度,沿AO向终点O移动;同时点N从点O出发,以每秒1.25个单位长度的速度,沿OB向终点B移动.当两个动点运动了x秒(0<x<4)时,解答下列问题: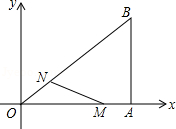
(1)求点N的坐标(用含x的代数式表示);
(2)设△OMN的面积是S,求S与x之间的函数表达式;当x为何值时,S有最大值?最大值是多少?
(3)在两个动点运动过程中,是否存在某一时刻,使△OMN是直角三角形?若存在,求出x的值;若不存在,请说明理由.
如图是某城市部分街道示意图,AF∥BC,EC⊥BC,BA∥DE,BD∥AE.甲、乙两人同时从B站乘车到F站.甲乘1路车,路线是B—A—E—F;乙乘2路车,路线是B—D—C—F.假设两车速度相同,途中耽误时间相同,那么谁先到达F站?请说明理由.
如图,在四边形ABCD中,∠ADC=∠B=90°,DE⊥AB,垂足为E,且DE=EB=5,请用割补(旋转图形)的方法求四边形ABCD的面积.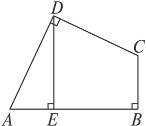
在某中学举行的电脑知识竞赛中,将参赛学生的成绩(得分均为整数)进行整理后分成五组,绘制出频数分布直方图,已知图中从左到右的第一、第三、第四、第五小组的频率分别是0.30,0.15,0.10,0.05,第二小组的频数是40.
(1)求第二小组的频率,并补全这个频数分布直方图;
(2)求参赛的学生的优秀率(成绩≥80为优秀)和及格率(成绩≥60为及格);
(3)参赛学生成绩的中位数应落在第几小组内?(不必说明理由)
(4)请你评价一下这次竞赛的成绩.
甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示: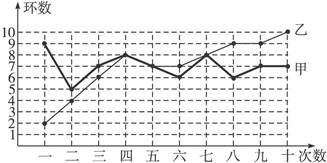
(1)请填写下表:
| 平均数 |
方差 |
中位数 |
命中9环及以上的次数 |
|
| 甲 |
7 |
1.2 |
1 |
|
| 乙 |
5.4 |
(2)请从下列四个不同的角度对这次测试结果进行分析:
①从平均数和方差相结合看;
②从平均数和中位数相结合看(分析谁的成绩好些);
③从平均数和命中9环以上的次数相结合看(分析谁的成绩好些);
④从折线图上两人射击命中环数的走势看(分析谁更有潜力).
甲、乙两位同学参加奥赛班11次测验成绩分布如图所示:(单位:分)
(1)他们的平均成绩分别是多少?
(2)他们测验成绩的方差、极差是多少?
(3)现要从中选出一人参加比赛,历届比赛表明,成绩达到98分以上才可进入决赛,你认为应选谁参加这次比赛,为什么?
(4)分析两位同学的成绩各有何特点?并对两位同学各提一条学习建议.