一水果经销商购进了A，B两种水果各10箱，分配给他的甲、乙两-优题课

一水果经销商购进了A，B两种水果各10箱，分配给他的甲、乙两个零售店（分别简称甲店、乙店）销售，预计每箱水果的盈利情况如下表：

（1）如果甲、乙两店各配货10箱，其中A种水果两店各5箱，B种水果两店各5箱，请你计算出经销商能盈利多少元？
（2）在甲、乙两店各配货10箱（按整箱配送），且保证乙店盈利不小于100元的条件下，请你设计出使水果经销商盈利最大的配货方案，并求出最大盈利为多少？

科目数学题型解答题难度中等

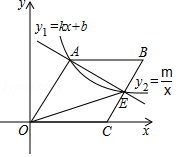
$▱ ABCO$ 在平面直角坐标系中的位置如图所示，直线 $y_{1} = kx + b$ 与双曲线 $y_{2} = \frac{m}{x} (m > 0)$ 在第一象限的图象相交于 $A$ 、 $E$ 两点，且 $A (3, 4)$ ， $E$ 是 $BC$ 的中点．

（1）连接 $OE$ ，若 $ΔABE$ 的面积为 $S_{1}$ ， $ΔOCE$ 的面积为 $S_{2}$ ，则 $S_{1}$ 　 $=$ 　 $S_{2}$ （直接填“ $>$ ”“ $<$ ”或“ $=$ ” $)$ ；

（2）求 $y_{1}$ 和 $y_{2}$ 的解析式；

（3）请直接写出当 $x$ 取何值时 $y_{1} > y_{2}$ ．

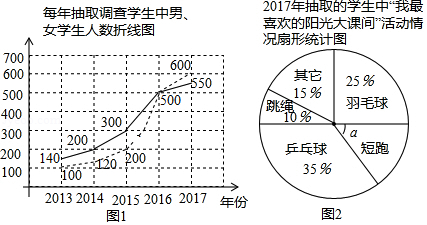
西昌市教科知局从2013年起每年对全市所有中学生进行“我最喜欢的阳光大课间活动”抽样调查（被调查学生每人只能选一项），并将抽样调查的数据绘制成图1、图2两幅统计图，根据统计图提供的信息解答下列问题：

（1）　　年抽取的调查人数最少；　　年抽取的调查人数中男生、女生人数相等；

（2）求图2中“短跑”在扇形图中所占的圆心角 $α$ 的度数；

（3）2017年抽取的学生中，喜欢羽毛球和短跑的学生共有多少人？

（4）如果2017年全市共有3.4万名中学生，请你估计我市2017年喜欢乒乓球和羽毛球两项运动的大约有多少人？

在 $▱ ABCD$ 中， $E$ 、 $F$ 分别是 $AD$ 、 $BC$ 上的点，将平行四边形 $ABCD$ 沿 $EF$ 所在直线翻折，使点 $B$ 与点 $D$ 重合，且点 $A$ 落在点 $A'$ 处．

（1）求证：△ $A' ED ≅ ΔCFD$ ；

（2）连接 $BE$ ，若 $∠ EBF = 60 °$ ， $EF = 3$ ，求四边形 $BFDE$ 的面积．

如图，在平面直角坐标系中，抛物线 $y = a x^{2} + bx + c$ 交 $x$ 轴于 $A$ 、 $B$ 两点，交 $y$ 轴于点 $C (0, - \frac{4}{3})$ ， $OA = 1$ ， $OB = 4$ ，直线 $l$ 过点 $A$ ，交 $y$ 轴于点 $D$ ，交抛物线于点 $E$ ，且满足 $\tan ∠ OAD = \frac{3}{4}$ ．

（1）求抛物线的解析式；

（2）动点 $P$ 从点 $B$ 出发，沿 $x$ 轴正方向以每秒2个单位长度的速度向点 $A$ 运动，动点 $Q$ 从点 $A$ 出发，沿射线 $AE$ 以每秒1个单位长度的速度向点 $E$ 运动，当点 $P$ 运动到点 $A$ 时，点 $Q$ 也停止运动，设运动时间为 $t$ 秒．

①在 $P$ 、 $Q$ 的运动过程中，是否存在某一时刻 $t$ ，使得 $ΔADC$ 与 $ΔPQA$ 相似，若存在，求出 $t$ 的值；若不存在，请说明理由．

②在 $P$ 、 $Q$ 的运动过程中，是否存在某一时刻 $t$ ，使得 $ΔAPQ$ 与 $ΔCAQ$ 的面积之和最大？若存在，求出 $t$ 的值；若不存在，请说明理由．

已知 $Rt Δ ABC$ 中， $∠ ACB = 90 °$ ，点 $D$ 、 $E$ 分别在 $BC$ 、 $AC$ 边上，连接 $BE$ 、 $AD$ 交于点 $P$ ，设 $AC = kBD$ ， $CD = kAE$ ， $k$ 为常数，试探究 $∠ APE$ 的度数：

（1）如图1，若 $k = 1$ ，则 $∠ APE$ 的度数为　　；

（2）如图2，若 $k = \sqrt{3}$ ，试问（1）中的结论是否成立？若成立，请说明理由；若不成立，求出 $∠ APE$ 的度数．

（3）如图3，若 $k = \sqrt{3}$ ，且 $D$ 、 $E$ 分别在 $CB$ 、 $CA$ 的延长线上，（2）中的结论是否成立，请说明理由．