(南充)反比例函数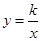 (
(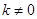 )与一次函数
)与一次函数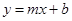
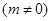 交于点A(1,
交于点A(1,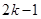 ).
).
(1)求反比例函数的解析式;
(2)若一次函数与x轴交于点B,且△AOB的面积为3,求一次函数的解析式.
计算:cos30°
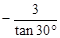 ;
;解方程: x(x+3)=2x+1
结合数轴与绝对值的知识回答下列问题: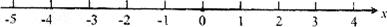
数轴上表示1和4的两点之间的距离是_________;表示-3和2的两点之间的距离是_________;表示-5和-4的两点之间的距离是_________;一般地,数轴上表示数
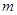 和数
和数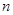 的两点之间的距离等于_____________.
的两点之间的距离等于_____________.如果表示数
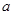 和-2的两点之间的距离是3,那么
和-2的两点之间的距离是3,那么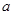 =__________.
=__________.若数轴上表示数
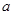 的点位于-4与2之间,求
的点位于-4与2之间,求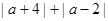 的值;
的值;当
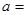 ______时,
______时,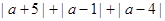 的值最小,最小值是____________
的值最小,最小值是____________
某市为组织开展第十五个“全国中小学安全教育日”活动,某中学举行了“全市中小学紧急疏散演练观摩会”.演练在一栋3层且每层楼有8间教室的教学楼中进行.教学楼共有3道门(两道大小相同的正门和一道侧门),在演练前,对这3道门进行了测试:当同时开启一正门和一道侧门时,半分钟内可以通过100名学生,若一道正门平均每分钟比一道侧门可多通过40名学生.求平均每分钟一道正门和一道侧门各可以通过多少名学生?
测试中发现,紧急情况时因学生拥挤,出门的效率会降低20%,假设这栋教学楼每间教室平均有45名学生,在紧急情况下,全楼的学生能否在5分钟内通过这3道门安全撤离?并说明理由.
如图,O是直线AB上一点,OC为任一条射线,OD平分∠AOC;OE平分∠BOC.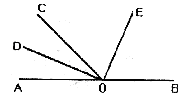
写出图中∠BOD与∠AOE的补角;
如果∠COD=25°,那么∠COE=_______;如果∠COD=60°,那么∠COE=________;
试猜想∠COD与∠COE具有怎样的数量关系,并说明理由.
2010年12月28日,国家财政部正式发布:自2011年1月1日起,排量再1.6升以下的汽车购置税由7.5%恢复至10%。王林在2010年12月30日购得一辆1.6升以下的小型货车,比在2011年1月1日后购买节省购置税1000元;根据国家“汽车下乡”的惠农政策,同时可以获得得汽车原价10%的政府补贴。问汽车原价为多少元?
王林可以领取多少元的政府补贴?