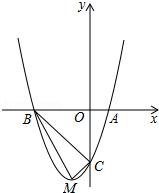
（宜宾）如图，在平面直角坐标系中，四边形ABCD是矩形，AD-优题课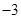

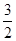（宜宾）如图，在平面直角坐标系中，四边形ABCD是矩形，AD∥x轴，A（，），AB=1，AD=2．
（1）直接写出B、C、D三点的坐标；
（2）将矩形ABCD向右平移m个单位，使点A、C恰好同时落在反比例函数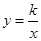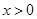（）的图象上，得矩形A′B′C′D′．求矩形ABCD的平移距离m和反比例函数的解析式．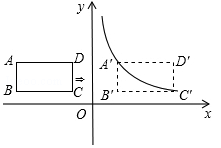

科目数学题型解答题难度中等

随着国家“惠民政策”的陆续出台，为了切实让老百姓得到实惠，国家卫计委通过严打药品销售环节中的不正当行为，某种药品原价200元 $/$ 瓶，经过连续两次降价后，现在仅卖98元 $/$ 瓶，现假定两次降价的百分率相同，求该种药品平均每次降价的百分率．

如图，方格中，每个小正方形的边长都是单位1， $ΔABC$ 在平面直角坐标系中的位置如图．

（1）画出将 $ΔABC$ 向右平移2个单位得到△ $A_{1} B_{1} C_{1}$ ；

（2）画出将 $ΔABC$ 绕点 $O$ 顺时针方向旋转 $90 °$ 得到的△ $A_{2} B_{2} C_{2}$ ；

（3）求△ $A_{1} B_{1} C_{1}$ 与△ $A_{2} B_{2} C_{2}$ 重合部分的面积．

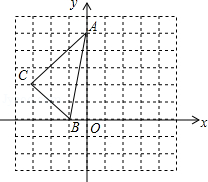
为了解中考考生最喜欢做哪种类型的英语客观题，2015年志愿者奔赴全市中考各考点对英语客观题的“听力部分、单项选择、完型填空、阅读理解、口语应用”进行了问卷调查，要求每位考生都自主选择其中一个类型，为此随机调查了各考点部分考生的意向．并将调查结果绘制成如图的统计图表（问卷回收率为 $100 %$ ，并均为有效问卷）．

被调查考生选择意向统计表

题型	所占百分比
听力部分	$a$
单项选择	$35 %$
完型填空	$b$
阅读理解	$10 %$
口语应用	$c$

根据统计图表中的信息，解答下列问题：

（1）求本次被调查的考生总人数及 $a$ 、 $b$ 、 $c$ 的值；

（2）将条形统计图补充完整；

（3）全市参加这次中考的考生共有42000人，试估计全市考生中最喜欢做“单项选择”这类客观题的考生有多少人？

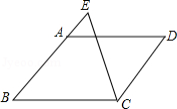
已知：如图，四边形 $ABCD$ 是平行四边形，延长 $BA$ 至点 $E$ ，使 $AE + CD = AD$ ．连接 $CE$ ，求证： $CE$ 平分 $∠ BCD$ ．

如图，顶点为 $M$ 的抛物线 $y = a {(x + 1)}^{2} - 4$ 分别与 $x$ 轴相交于点 $A$ ， $B$ （点 $A$ 在点 $B$ 的右侧），与 $y$ 轴相交于点 $C (0, - 3)$ ．

（1）求抛物线的函数表达式；

（2）判断 $ΔBCM$ 是否为直角三角形，并说明理由．

（3）抛物线上是否存在点 $N$ （点 $N$ 与点 $M$ 不重合），使得以点 $A$ ， $B$ ， $C$ ， $N$ 为顶点的四边形的面积与四边形 $ABMC$ 的面积相等？若存在，求出点 $N$ 的坐标；若不存在，请说明理由．