（资阳）如图，直线
与x轴、y轴分别相交于A、B两点，与双曲线
（
）相交于点P，PC⊥x轴于点C，且PC=2，点A的坐标为（﹣2，0）．
（1）求双曲线的解析式；
（2）若点Q为双曲线上点P右侧的一点，且QH⊥x轴于H，当以点Q、C、H为顶点的三角形与△AOB相似时，求点Q的坐标．
（·辽宁营口）【问题探究】
（1）如图1，锐角△ABC中，分别以AB、AC为边向外作等腰△ABE和等腰△ACD，使AE=AB，AD=AC，∠BAE=∠CAD，连接BD，CE，试猜想BD与CE的大小关系，并说明理由．
【深入探究】
（2）如图2，四边形ABCD中，AB=7cm，BC=3cm，∠ABC=∠ACD=∠ADC=45º，求BD的长．
（3）如图3，在（2）的条件下，当△ACD在线段AC的左侧时，求BD的长．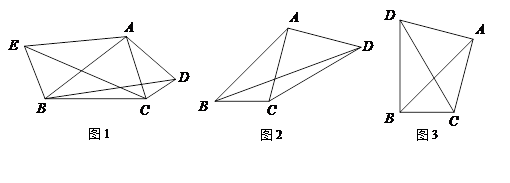
（·辽宁营口）如图，我南海某海域A处有一艘捕鱼船在作业时突遇特大风浪，船长马上向我国渔政搜救中心发出求救信号，此时一艘渔政船正巡航到捕鱼船正西方向的B处，该渔政船收到渔政求救中心指令后前去救援，但两船之间有大片暗礁，无法直线到达，于是决定马上调整方向，先向北偏东60º方向以每小时30海里的速度航行半小时到达C处，同时捕鱼船低速航行到A点的正北1．5海里D处，渔政船航行到点C处时测得点D在南偏东53º方向上．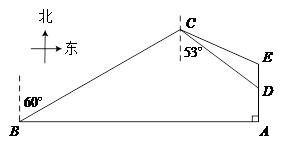
（1）求CD两点的距离；
（2）渔政船决定再次调整航向前去救援，若两船航速不变，并且在点E处相会合，求∠ECD的正弦值．
（参考数据：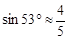
，
，
）
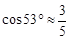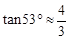（·湖北荆门，21题，分）如图，在一次军事演习中，蓝方在一条东西走向的公路上的A处朝正南方向撤退，红方在公路上的B处沿南偏西60°方向前进实施拦截，红方行驶1000米到达C处后，因前方无法通行，红方决定调整方向，再朝南偏西45°方向前进了相同的距离，刚好在D处成功拦截蓝方，求拦截点D处到公路的距离（结果不取近似值）．
（·辽宁葫芦岛）如图，小岛A在港口B的北偏东50°方向，小岛C在港口B的北偏西25°方向，一艘轮船以每小时20海里的速度从港口B出发向小岛A航行，经过5小时到达小岛A，这时测得小岛C在小岛A的北偏西70°方向，求小岛A距离小岛C有多少海里？（最后结果精确到1海里，参考数据：
≈1．414，
≈1．732）
（·辽宁沈阳）我国是世界上严重缺失的国家之一，全国总用水量逐年上升，全国总用水量可分为农业用水量、工业用水量和生活用水量三部分．为了合理利用水资源，我国连续多年对水资源的利用情况进行跟踪调查，将所得数据进行处理，绘制了2008年全国总用水量分布情况扇形统计图和2004﹣2008年全国生活用水量折线统计图的一部分如下：
（1）2007年全国生活用水量比2004年增加了16%，则2004年全国生活用水量为 亿m3，2008年全国生活用水量比2004年增加了20%，则2008年全国生活用水量为 亿m3；
（2）根据以上信息，请直接在答题卡上补全折线统计图；
（3）根据以上信息2008年全国总水量为 亿；
（4）我国2008年水资源总量约为2．75×104亿m3，根据国外的经验，一个国家当年的全国总用水量超过这个国家年水资源总量的20%，就有可能发生“水危机”．依据这个标准，2008年我国是否属于可能发生“水危机”的行列？并说明理由．