(·温州卷 第20题 8分)各顶点都在方格纸格点(横竖格子线的交错点)上的多边形称为格点多边形。如何计算它的面积?奥地利数学家皮克(G.Pick,1859~1942)证明了格点多边形的面积公式: ,其中
,其中 表示多边形内部的格点数,
表示多边形内部的格点数, 表示多边形边界上的格点数,S表示多边形的面积。如图,
表示多边形边界上的格点数,S表示多边形的面积。如图, ,
,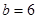 ,
, 。
。
(1)请在图甲中画一个格点正方形,使它内部只含有4个格点,并写出它的面积;
(2)请在图乙中画一个格点三角形,使它的面积为 ,且每条边上除顶点外无其它格点。(注:图甲、图乙在答题纸上)
,且每条边上除顶点外无其它格点。(注:图甲、图乙在答题纸上)
已知实数 、 满足 ,求代数式 的值.
计算 .
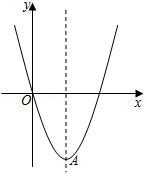
如图,在平面直角坐标系中,抛物线 经过原点 ,顶点为 .
(1)求抛物线的函数解析式;
(2)设点 为抛物线 的对称轴上的一点,点 在该抛物线上,当四边
形 为菱形时,求出点 的坐标;
(3)在(2)的条件下,抛物线 在第一象限的图象上是否存在一点 ,使得点 到直线 的距离与其到 轴的距离相等?若存在,求出直线 的函数解析式;若不存在,请说明理由.
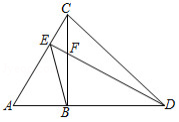
如图, 中, , 为 延长线上一点, ,过点 作 于点 ,交 于点 ,连接 , .
(1)求证: ;
(2)求 的度数;
(3)当 时,求 的值.
某商店销售一种商品,每件的进价为50元,经市场调研发现,当该商品每件的售价为60元时,每天可销售200件;当售价高于进价时,每件的售价每增加1元,每天的销售数量将减少10件.
(1)当每件商品的售价为64元时,求该商品每天的销售数量;
(2)当每件商品的售价为多少时,销售该商品每天获得的利润最大?并求出最大利润.