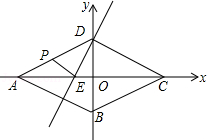
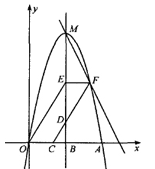
(·温州卷 第23题 12分)如图,抛物线 交
交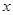 轴正半轴于点A,顶点为M,对称轴NB交
轴正半轴于点A,顶点为M,对称轴NB交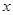 轴于点B,过点C(2,0)作射线CD交MB于点D(D在
轴于点B,过点C(2,0)作射线CD交MB于点D(D在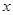 轴上方),OE∥CD交MB于点E,EF∥
轴上方),OE∥CD交MB于点E,EF∥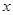 轴交CD于点F,作直线MF。
轴交CD于点F,作直线MF。
(1)求点A,M的坐标;
(2)当BD为何值时,点F恰好落在抛物线上?
(3)当BD=1时,①、求直线MF的解析式,并判断点A是否落在该直线上;
②、延长OE交FM于点G,取CF中点P,连结PG,△FPG,四边形DEGP,四边形OCDE的面积分别记为S1,S2,S3,则S1:S2:S3= .
如图,直线 与双曲线相交于点 ,与 轴交于点 .
(1)求双曲线解析式;
(2)点 在 轴上,如果 的面积为3,求点 的坐标.

已知关于 的一元二次方程 有实数根.
(1)求 的取值范围;
(2)如果方程的两个实数根为 , ,且 ,求 的取值范围.
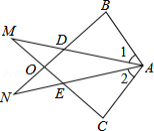
已知 和 位置如图所示, , , .
(1)求证: ;
(2)求证: .
在校园文化艺术节中,九年级一班有1名男生和2名女生获得美术奖,另有2名男生和2名女生获得音乐奖.
(1)从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会,求刚好是男生的概率;
(2)分别从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会,用列表或树状图求刚好是一男生一女生的概率.
如图,以菱形 对角线交点为坐标原点,建立平面直角坐标系, 、 两点的坐标分别为 , 、 ,直线 交 于 ,动点 从点 出发,以每秒2个单位的速度沿着 的路线向终点 匀速运动,设 的面积为 ,点 的运动时间为 秒.
(1)求直线 的解析式;
(2)求 与 之间的函数关系式,并写出自变量 的取值范围;
(3)当 为何值时, ?并求出此时直线 与直线 所夹锐角的正切值.