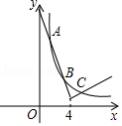
（·湖北黄冈，24题，分）（14 分）如图，在矩形OABC 中，OA=5，AB=4，点D 为边AB 上一点，将△BCD 沿直线CD 折叠，使点B 恰好落在OA边上的点E 处，分别以OC，OA 所在的直线为x 轴，y 轴建立平面直角坐标系．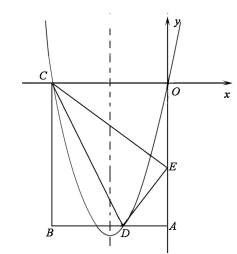
（1）求OE 的长；
（2）求经过O，D，C 三点的抛物线的解析式；
（3）一动点P 从点C 出发，沿CB 以每秒2 个单位长的速度向点B 运动，同时动点Q 从E 点出发，沿EC 以每秒1 个单位长的速度向点C 运动，当点P 到达点B 时，两点同时停止运动．设运动时间为t 秒，当t为何值时，DP=DQ；
（4） 若点N 在（2）中的抛物线的对称轴上，点M 在抛物线上，是否存在这样的点M与点N，使得以M，N，C，E 为顶点的四边形是平行四边形？若存在，请求出M 点的坐标；若不存在，请说明理由．
学校为了调查学生对教学的满意度，随机抽取了部分学生作问卷调查：用“A”表示“很满意“，“B”表示“满意”，“C”表示“比较满意”，“D”表示“不满意”，如图甲、乙是工作人员根据问卷调查统计资料绘制的两幅不完整的统计图，请你根据统计图提供的信息解答以下问题：
（1）本次问卷调查，共调查了多少名学生？
（2）将图甲中“B”部分的图形补充完整；
（3）如果该校有学生1000人，请你估计该校学生对教学感到“不满意”的约有多少人？
如图，小红同学用仪器测量一棵大树AB的高度，在C处测得∠ADG=30°，在E处测得∠AFG=60°，CE=8米，仪器高度CD=1.5米，求这棵树AB的高度（结果保留两位有效数字，
≈1.732）．
先化简：
，再请你选择一个合适的数作为x的值代入求值．
如图，在平面直角坐标系中，直线y=
x+1分别与两坐标轴交于B，A两点，C为该直线上的一动点，以每秒1个单位长度的速度从点A开始沿直线BA向上移动，作等边△CDE，点D和点E都在x轴上，以点C为顶点的抛物线y=a（x﹣m）2+n经过点E．⊙M与x轴、直线AB都相切，其半径为3（1﹣
）a．
（1）求点A的坐标和∠ABO的度数；
（2）当点C与点A重合时，求a的值；
（3）点C移动多少秒时，等边△CDE的边CE第一次与⊙M相切？
如图，在直角梯形ABCD中，AD∥BC，∠ABC=90°．点E为底AD上一点，将△ABE沿直线BE折叠，点A落在梯形对角线BD上的G处，EG的延长线交直线BC于点F．
（1）点E可以是AD的中点吗？为什么？
（2）求证：△ABG∽△BFE；
（3）设AD=a，AB=b，BC=c
①当四边形EFCD为平行四边形时，求a，b，c应满足的关系；
②在①的条件下，当b=2时，a的值是唯一的，求∠C的度数．