某校为了丰富学生的第二课堂,对学生参与演讲、舞蹈、书法和摄影活动的兴趣情况进行调查,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中最感兴趣的一项),对调查结果进行统计后,绘制了如下两个统计图:
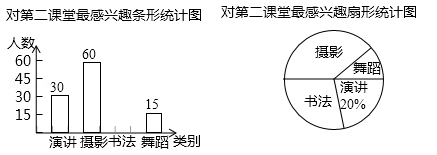
(1)此次调查抽取的学生人数m= 名,其中选择“书法”的学生占抽样人数的百分比n= ;
(2)若该校有3000名学生,请根据以上数据估计该校对“书法”最感兴趣的学生人数.
张欣和李明相约到图书城去买书.请你根据他们的对话内容,求出李明上次所买书籍的原价.
解方程:
化简:
如图,正方形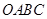 的面积为9,点
的面积为9,点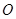 为坐标原点,点
为坐标原点,点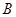 在函数
在函数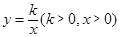 的图象上,点
的图象上,点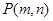 是函数
是函数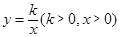 的图象上任意一点,边点
的图象上任意一点,边点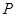 分别作
分别作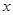 轴、
轴、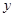 轴的垂线,垂足分别为
轴的垂线,垂足分别为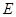 、
、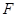 ,并设矩形
,并设矩形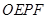 和正方形
和正方形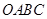 不重合部分的面积为S.
不重合部分的面积为S.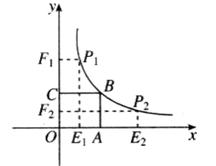
⑴求
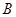 点的坐标和
点的坐标和 的值;
的值;⑵当
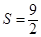 时,求
时,求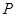 点的坐标;
点的坐标;⑶写出
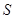 关于
关于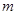 的函数关系式.
的函数关系式.
如图,在直角坐标系中,已知直线y=kx+6与x轴、y轴分别交于A、B两点,且△ABO的面积为12.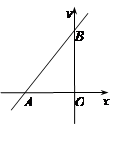
(1)求k的值;
(2)若P为直线AB上一动点,P点运动到什么位置时,△PAO是以OA为底的等腰三角形,求点P的坐标;
(3)在(2)的条件下,连结PO,△PBO是等腰三角形吗?如果是,试说明理由,如果不是,请在线段AB上求一点C,使得△CBO是等腰三角形.