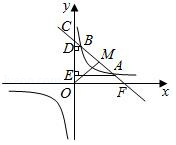
如图,在边长为1的小正方形网格中,三角形的三个顶点均落在格点上.
(1)以三角形的其中两边为边画一个平行四边形,并在顶点处标上字母A,B,C,D;
(2)证明四边形ABCD是平行四边形.
计算: .
如图,在以点 为中心的正方形 中, ,连接 ,动点 从点 出发沿 以每秒1个单位长度的速度匀速运动,到达点 停止.在运动过程中, 的外接圆交 于点 ,连接 交 于点 ,连接 ,将 沿 翻折,得到 .
(1)求证: 是等腰直角三角形;
(2)当点 恰好落在线段 上时,求 的长;
(3)设点 运动的时间为 秒, 的面积为 ,求 关于时间 的关系式.

在平面直角坐标系中,将二次函数 的图象向右平移1个单位,再向下平移2个单位,得到如图所示的抛物线,该抛物线与 轴交于点 、 (点 在点 的左侧), ,经过点 的一次函数 的图象与 轴正半轴交于点 ,且与抛物线的另一个交点为 , 的面积为5.
(1)求抛物线和一次函数的解析式;
(2)抛物线上的动点 在一次函数的图象下方,求 面积的最大值,并求出此时点 的坐标;
(3)若点 为 轴上任意一点,在(2)的结论下,求 的最小值.

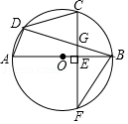
如图, 是 的直径,点 为 的中点, 为 的弦,且 ,垂足为 ,连接 交 于点 ,连接 , , .
(1)求证: ;
(2)若 ,求 的长.
如图,一次函数 的图象与反比例函数 且 的图象在第一象限交于点 、 ,且该一次函数的图象与 轴正半轴交于点 ,过 、 分别作 轴的垂线,垂足分别为 、 .已知 , .
(1)求 的值和反比例函数的解析式;
(2)若点 为一次函数图象上的动点,求 长度的最小值.