(黔西南州)如图,点P在⊙O外,PA、PB分别与⊙O相切于A、B两点,∠P=50°,则∠AOB等于( )
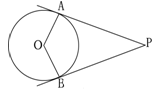
A.150° B.130° C.155° D.135°
一个点从数轴的-1所表示的点开始,先向左移动5个单位,再向右移动3个单位,这时该点表示的数是()
| A.1 | B.-2 | C.-5 | D.-3 |
-3的相反数是()
| A.3 | B.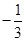 |
C.—3 | D.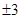 |
校运动会上,初二(3)班啦啦队买了两种价格的雪糕,其中甲种雪糕共花费40元,乙种雪糕共花费30元,甲种雪糕比乙种雪糕多20根.乙种雪糕价格是甲种雪糕价格的1.5倍,若设甲种雪糕的价格为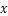 元,根据题意可列方程为()
元,根据题意可列方程为()
A.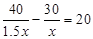 |
B. |
C.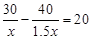 |
D.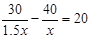 |
解分式方程 ,去分母后所得的方程是()
,去分母后所得的方程是()
A.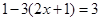 |
B. |
C. |
D.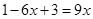 |
已知在△ABC中有两个角的大小分别为40°和70°,则这个三角形是
| A.直角三角形 | B.等边三角形 | C.钝角三角形 | D.等腰三角形 |