如图,已知在△ABC中,∠A=90°,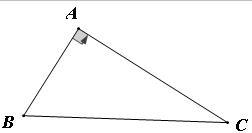
(1)请用圆规和直尺作出⊙P,使圆心P在AC边上,且与AB,BC两边都相切(保留作图痕迹,不写作法和证明).
(2)若∠B=60°,AB=3,求⊙P的面积.
(本题5分)如图所示,已知BD⊥CD于D,EF⊥CD于F, ,
,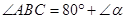 ,其中
,其中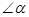 为锐角,求证:
为锐角,求证: 。
。
(本题7分)如图,已知A (4,a),B (﹣2,﹣4)是一次函数y=kx+b的图象和反比例函数y=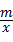 的图象的交点.
的图象的交点.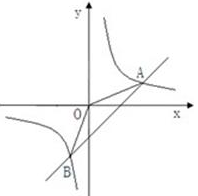
(1)求反比例函数和一次函数的解祈式;
(2)求△A0B的面积.
(本题13分)已知:在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合).以AD为边作正方形ADEF,连接CF.
(1)如图1,当点D在线段BC上时,求证:①BD⊥CF.②CF=BC﹣CD.
(2)如图2,当点D在线段BC的延长线上时,其它条件不变,请直接写出CF、BC、CD三条线段之间的关系;
(3)如图3,当点D在线段BC的反向延长线上时,且点A、F分别在直线BC的两侧,其它条件不变:①请直接写出CF、BC、CD三条线段之间的关系.②若连接正方形对角线AE、DF,交点为O,连接OC,探究△AOC的形状,并说明理由.
(本题12分)如图,直线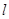 :
: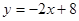 分别与
分别与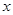 轴、
轴、 轴交于A、B两点,点C线段AB上,作CD⊥x轴于D, CD="2OD," 点E线段OB上,且AE=BE;
轴交于A、B两点,点C线段AB上,作CD⊥x轴于D, CD="2OD," 点E线段OB上,且AE=BE;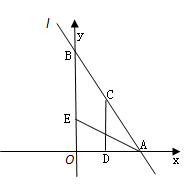
(1)填空:点C的坐标为( , );点E的坐标为( , );
(2)直线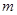 过点E,且将△AOB分成面积比为1:2的两部分,求直线
过点E,且将△AOB分成面积比为1:2的两部分,求直线 的表达式;
的表达式;
(3)点P在x轴上运动,
①当PC+PE取最小值时,求点P的坐标及PC+PE的最小值;
②当PC-PE取最大值时,求点P的坐标及PC-PE的最大值;
(本题10分)某医药研究所开发一种新药.在试验药效时发现,如果成人按规定剂量服用,那么服药2h后血液中含药量最高,达到每毫升6μg(1μg=10-3mg),接着逐步衰减,10h后血液中含药量为每毫升3μg.若每毫升血液中含药量y(μg)随时间x(h)的变化如图所示,则当成人按规定剂量服药后: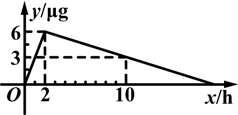
(1)分别求出0≤x≤2和x>2时,y与x之间的函数解析式;
(2)如果每毫升血液中含药量为4μg或4μg以上时药物对疾病的治疗是有效的,那么这个有效时间是多长?