(本小题满分12分)已知直线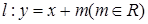 ,双曲线
,双曲线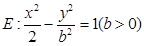 .
.
①若直线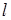 与双曲线
与双曲线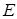 的其中一条渐近线平行,求双曲线
的其中一条渐近线平行,求双曲线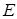 的离心率;②若直线
的离心率;②若直线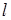 过双曲线的右焦点
过双曲线的右焦点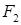 ,与双曲线交于
,与双曲线交于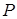 、
、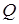 两点,且
两点,且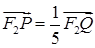 ,求双曲线方程.
,求双曲线方程.
(本小题满分13分)已知函数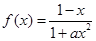 ,其中
,其中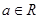 .
.
(1)当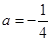 时,求
时,求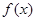 的单调区间;
的单调区间;
(2)当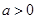 时,证明:存在实数
时,证明:存在实数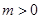 ,使得对于任意的实数
,使得对于任意的实数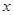 ,都有
,都有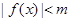 成立.
成立.
(本小题满分14 分)如图1,在边长为4的菱形 中,
中, ,
, 于点
于点 ,将
,将 沿
沿 折起到
折起到 的位置,使
的位置,使 ,如图 2.
,如图 2.

(1)求证: 平面
平面 ;
;
(2)求二面角 的余弦值;
的余弦值;
(3)判断在线段 上是否存在一点
上是否存在一点 ,使平面
,使平面 平面
平面 ?若存在,求出
?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(本小题满分13 分)某厂商调查甲、乙两种不同型号电视机在10 个卖场的销售量(单位:台),并根据这10个卖场的销售情况,得到如图所示的茎叶图.
为了鼓励卖场,在同型号电视机的销售中,该厂商将销售量高于数据平均数的卖场命名为该型号电视机的“星级卖场”.
(1)当 时,记甲型号电视机的“星级卖场”数量为
时,记甲型号电视机的“星级卖场”数量为 ,乙型号电视机的“星级卖场”数量为
,乙型号电视机的“星级卖场”数量为 ,比较
,比较 ,
, 的大小关系;
的大小关系;
(2)在这10 个卖场中,随机选取2 个卖场,记 为其中甲型号电视机的“星级卖场”的个数,求
为其中甲型号电视机的“星级卖场”的个数,求 的分布列和数学期望;
的分布列和数学期望;
(3)若 ,记乙型号电视机销售量的方差为
,记乙型号电视机销售量的方差为 ,根据茎叶图推断
,根据茎叶图推断 为何值时,
为何值时, 达到最小值.(只需写出结论)
达到最小值.(只需写出结论)
(本小题满分13分)在锐角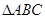 中,角
中,角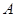 ,
,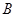 ,
, 所对的边分别为
所对的边分别为 ,
, ,
,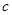 ,已知
,已知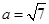 ,
, ,
, .
.
(1)求角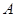 的大小;
的大小;
(2)求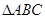 的面积.
的面积.
一束光线通过点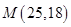 射到
射到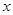 轴上,被反射到圆
轴上,被反射到圆
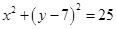 上.
上.
(1)求通过圆心的反射光线所在直线方程;
(2)求在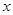 轴上入射点
轴上入射点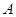 的活动范围.
的活动范围.