(本小题满分12分)已知函数 在点
在点 的切线方程为
的切线方程为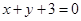 .
.
(1)求函数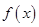 的解析式;
的解析式;
(2)设 时,求证:
时,求证: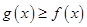 ;
;
(3)已知 ,求证:
,求证: .
.
已知二项式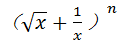 的展开式中各项系数的和为64.
的展开式中各项系数的和为64.
(I)求n;
(II)求展开式中的常数项.
(本小题满分14分)
已知函数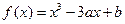 在
在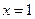 处有极小值
处有极小值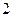 。
。
(1)求函数 的解析式;
的解析式;
(2)若函数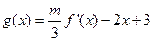 在
在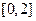 只有一个零点,求
只有一个零点,求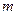 的取值范围。
的取值范围。
(本小题满分14分)
如图,在 中,
中, ,以
,以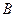 、
、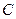 为焦点的椭圆恰好过
为焦点的椭圆恰好过 的中点
的中点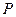 。
。
(1)求椭圆的标准方程;
(2)过椭圆的右顶点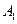 作直线
作直线 与圆
与圆 相交于
相交于 、
、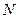 两点,试探究点
两点,试探究点 、
、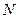 能将圆
能将圆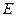 分割成弧长比值为
分割成弧长比值为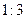 的两段弧吗?若能,求出直线
的两段弧吗?若能,求出直线 的方程;若不能,请说明理由.
的方程;若不能,请说明理由.
(本小题满分14分)
已知数列 的前
的前 项和
项和 满足
满足 ,等差数列
,等差数列 满足
满足 ,
, 。
。
(1)求数列 、
、 的通项公式;
的通项公式;
(2)设 ,数列
,数列 的前
的前 项和为
项和为 ,问
,问 >
> 的最小正整数
的最小正整数 是多少?
是多少?
(本小题满分14分)
如图的几何体中, 平面
平面 ,
,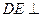 平面
平面 ,△
,△ 为等边三角形
为等边三角形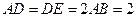 ,
, 为
为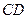 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求证:平面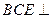 平面
平面 。
。