本题共有2个小题,第1小题满分6分,第2小题满分8分.
已知圆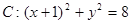 .
.
(1)求过点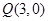 的圆C的切线
的圆C的切线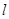 的方程;
的方程;
(2)如图,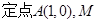 为圆C上一动点,点P在AM上,点N在CM上,且满足
为圆C上一动点,点P在AM上,点N在CM上,且满足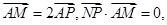 求
求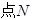 的轨迹.
的轨迹.
(本小题满分10分)已知数集A={a1,a2, ,an}(0≤a1<a2< <an,n≥2,n∈N*)具有性质P:"i,j(1≤i≤j≤n),
ai+aj与aj-ai两数中至少有一个属于A.
(1)分别判断数集{1,2,3,4}是否具有性质P,并说明理由;
(2)证明:a1=0;
(3)证明:当n=5时,a1,a2,a3,a4,a5成等差数列.
(本小题满分10分)已知箱中装有2个白球,3个黑球,每次从中任取一球(不放回),取完白球则停止取球.
(1)求取2次后仍不能停止的概率;
(2)记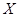 为停止取球后取球的次数,求
为停止取球后取球的次数,求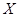 的数学期望
的数学期望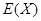 .
.
【选修4—5:不等式选讲】(本小题满分10分)
已知a,b,c>0,且a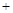 b
b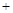 c
c  1,求证:
1,求证: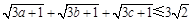 .
.
【选修4—4:坐标系与参数方程】(本小题满分10分)
在极坐标系中,设直线 过点
过点 ,
,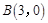 ,且直线
,且直线 与曲线
与曲线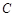 :
:
有公共点,求实数 的最小值.
的最小值.
【选修4—2:矩阵与变换】(本小题满分10分)
已知点P(a,b),先对它逆时针旋转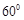 ,再作N
,再作N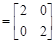 对应的变换,得到的点的坐标为(8,
对应的变换,得到的点的坐标为(8,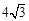 ),求实数a,b的值.
),求实数a,b的值.