（本题6分）阅读理解：
图1中的每相邻两条竖线之间，从上至下有若干条横线（即“桥”），这样就构成了“天梯”。现在规定，运算符号“×、÷、+、－”分别从它们下方的竖线上端出发，在“天梯”的竖线与横线上运动，它们在运动过程中按自上而下，且逢“桥”必过的规则进行，最后运动到竖线下方字母之间的“○”中，将a、b、c、d、e连接起来，构成一个算式．例如图1中，“×”号根据规则就应该沿箭头方向运动，最后向下进入d、e之间的“○”中，其余3个运算符号分别按规则运动到“○”中后，就得到算式：a－b+c÷d×e．
解决问题：
（1）根据图2所示的“天梯”写出算式，并计算当a=6，b=﹣32，c=﹣8，d=
，e=﹣
时所写算式的值；
（2）在图3添加横线（不超过4条），中设计出一种“天梯”，使列出的算式为a－b÷c×d+e．
（本题8分）某校七（2）班40名同学为“希望工程”捐款,共捐款100元。捐款情况如下表：
表格中捐款2元和3元的人数不小心被墨水污染已看不清楚，不过应用方程组可以解决这个问题。现在设捐款2元的有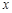
名同学,捐款3元的有
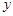名同学,请你列方程组并解出方程组。
（本题5分）若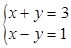方程组
与方程组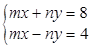
的解相同，求
、
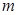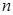的值。
（本题5分）解不等式组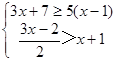
计算（本题每小题5分，共10分）：
（1）
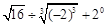
（2）
（本题10分）如图，方格纸中的每个小方格都是边长为1个单位长度的正方形，每个小正方形的顶点叫格点，△ABC和△DEF的顶点都在格点上，结合所给的平面直角坐标系解答下列问题：
（1）画出△ABC向上平移4个单位长度后所得到的△A1B1C1；
（2）画出△DEF绕点O按顺时针方向旋转90°后所得到的△D1E1F1；
（3）△A1B1C1和△D1E1F1组成的图形是轴对称图形吗？如果是，请画出对称轴.