设 为实数,函数
为实数,函数
(Ⅰ)当 时,求
时,求 在
在 上的最大值;
上的最大值;
(Ⅱ)设函数 ,当
,当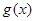 有两个极值点
有两个极值点 时,总有
时,总有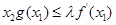 ,求实数
,求实数 的值。(
的值。(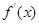 为
为 的导函数)
的导函数)
某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数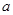 .
.
①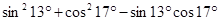 ;
;
②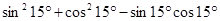 ;
;
③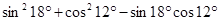 ;
;
④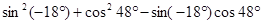 ;
;
⑤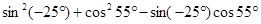 .
.
(1)从上述五个式子中选择一个,求出常数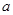 ;
;
(2)根据(1)的计算结果,将该同学的发现推广为一个三角恒等式,并证明你的结论.
已知函数 (
(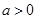 ).
).
(1)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(2)当 时,
时, 取得极值.
取得极值.
① 若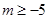 ,求函数
,求函数 在
在 上的最小值;
上的最小值;
② 求证:对任意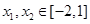 ,都有
,都有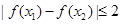 .
.
如图,过抛物线 的对称轴上任一点
的对称轴上任一点 作直线与抛物线交于
作直线与抛物线交于 、
、 两点,点Q是点P关于原点的对称点.
两点,点Q是点P关于原点的对称点.
(1)设 ,证明:
,证明: ;
;
(2)设直线AB的方程是 ,过
,过 、
、 两点的圆C与抛物线在点A处有共同的切线,求圆C的方程.
两点的圆C与抛物线在点A处有共同的切线,求圆C的方程.
已知函数
(1)若 求
求 在
在 处的切线方程;
处的切线方程;
(2)若 在区间
在区间 上恰有两个零点,求
上恰有两个零点,求 的取值范围.
的取值范围.
某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数 .
.
① ;
;
② ;
;
③ ;
;
④ ;
;
⑤ .
.
(1)从上述五个式子中选择一个,求出常数 ;
;
(2)根据(1)的计算结果,将该同学的发现推广为一个三角恒等式,并证明你的结论.