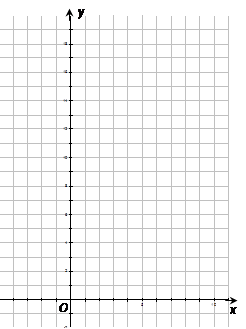
己知函数f(x)= +blnx+c(a>0)的图像在点(1,f(1))处的切线方程为x-y-2="0"
+blnx+c(a>0)的图像在点(1,f(1))处的切线方程为x-y-2="0"
(1)用a表示b,c;
(2)若函数g(x)=x-f(x)在x∈(0,1]上的最大值为2,求实数a的取值范围.
极坐标系的极点是直角坐标系的原点,极轴为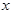 轴正半轴。已知曲线
轴正半轴。已知曲线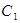 的极坐标方程为
的极坐标方程为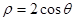 ,曲线
,曲线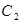 的参数方程为
的参数方程为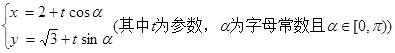
(1)求曲线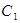 的直角坐标方程和曲线
的直角坐标方程和曲线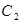 的普通方程;
的普通方程;
(2)当曲线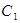 和曲线
和曲线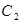 没有公共点时,求
没有公共点时,求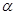 的取值范围。
的取值范围。
(本小题满分12分)在数列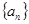 中,
中,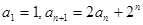 .
.
(1)设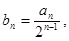 证明
证明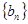 是等差数列;
是等差数列;
(2)求数列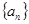 的前
的前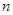 项和
项和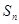 .
.
(本小题满分12分)等比数列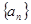 的前
的前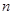 项和为
项和为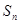 ,已知
,已知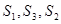 成等差数列.
成等差数列.
(1)求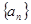 的公比
的公比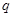
(2)若 ,求
,求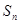 .
.
(本小题满分l2分)已知函数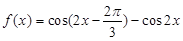 (
(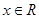 ).
).
(Ⅰ)求函数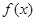 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;
(Ⅱ) 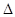
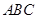 内角
内角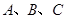 的对边长分别为
的对边长分别为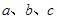 ,若
,若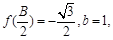
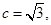 且
且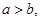 试求角B和角C.
试求角B和角C.
(本小题满分12分)某投资人打算投资甲、乙两个项目. 根据预测,甲、乙项目可能的最大盈利率分别为100﹪和50﹪,可能的最大亏损分别为30﹪和10﹪. 投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元. 问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?