(本题8分)全集U=R,若集合 ,
,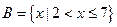 ,
,
则(结果用区间表示)
(1)求 ; (
; ( 2)若集合C=
2)若集合C= ,
,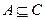 ,求
,求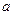 的取值范围;
的取值范围;
(本题8分,每小题各4分)
(1) ;(2)
;(2)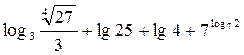
对于给定首项 ,由递推公式 得到数列 ,对于任意的 ,都有 ,用数列 可以计算 .
(1)取
,计算
的值(精确到0.01);归纳出
的大小关系;
(2)当
时,证明:
.
(3)当 时,用数列 计算 的近似值,要求 ,请你估计 ,并说明理由
定义域为
,且对任意实数
都满足不等式
的所有函数
组成的集合记为
,例如,函数
.
(1)已知函数
,证明:
;
(2)写出一个函数
,使得
,并说明理由;
(3)写出一个函数
,使得数列极限
.
已知抛物线
(1)
的三个顶点在抛物线
上,记
的三边
、
、
所在的直线的斜率分别为
,
,
若A的坐标在原点,求
的值;
(2)请你给出一个以
为顶点、其余各顶点均为抛物线
上的动点的多边形,写出各多边形各边所在的直线斜率之间的关系式,并说明理由