某化工厂生产的一种溶液,若初时含杂质2%,每过滤一次可使杂质含量减少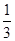 .(已知:
.(已知: ,
, )
)
(1)求杂质含量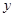 与过滤次数
与过滤次数 的函数关系式;
的函数关系式;
(2)按市场要求,杂质含量不能超过0.1%.问至少应过滤几次才能使产品达到市场要求?
(本小题满分12分)
已知函数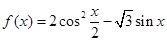 .
.
(1)求函数 的最小正周期和值域;
的最小正周期和值域;
(2)若 为第二象限角,且
为第二象限角,且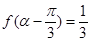 ,求
,求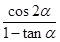 的值.
的值.
.(本小题满分15分)
已知函数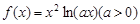
(Ⅰ)若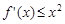 对任意的
对任意的 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(Ⅱ)当 时,设函数
时,设函数 ,若
,若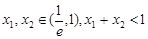 ,求证
,求证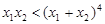
(本小题满分15分).
已知 、
、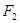 分别为椭圆
分别为椭圆 :
: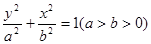 的
的
上、下焦点,其中 也是抛物线
也是抛物线 :
: 的焦点,
的焦点,
点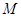 是
是 与
与 在第二象限的交点,且
在第二象限的交点,且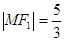 。
。
(Ⅰ)求椭圆的方程;
(Ⅱ)已知点P(1,3)和圆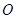 :
: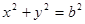 ,过点P的动直线
,过点P的动直线 与圆
与圆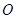 相交于不同的两点A,B,在线段AB取一点Q,满足:
相交于不同的两点A,B,在线段AB取一点Q,满足: ,
,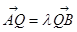 (
(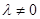 且
且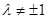 )。求证:点Q总在某定直线上。
)。求证:点Q总在某定直线上。
(本小题满分14分)
在长方体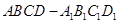 中,
中,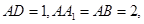 点
点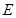 是
是 上的动点,点
上的动点,点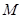 为
为 的中点.
的中点.
(Ⅰ)当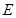 点在何处时,直线
点在何处时,直线 //平面
//平面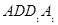 ,
,
并证明你的结论;
(Ⅱ)在(Ⅰ)成立的条件下,求二面角
的大小.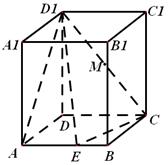
(本小题满分14分)
已知各项均为正数的数列{an}前n项和为Sn,(p – 1)Sn = p2 – an,n ∈N*,p > 0且p≠1,数列{bn}满足bn = 2logpan.
(Ⅰ)若p =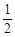 ,设数列
,设数列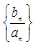 的前n项和为Tn,求证:0 < Tn≤4;
的前n项和为Tn,求证:0 < Tn≤4;
(Ⅱ)是否存在自然数M,使得当n > M时,an > 1恒成立?若存在,求出相应的M;若不存在,请说明理由.