设椭圆C: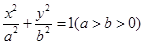 的离心率与双曲线
的离心率与双曲线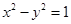 的离心率互为倒数,且椭圆C过点
的离心率互为倒数,且椭圆C过点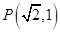 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若椭圆C的左、右焦点分别为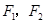 ,过
,过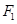 的直线
的直线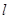 与椭圆C相交于A、B两点,求
与椭圆C相交于A、B两点,求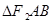 面积的最大值.
面积的最大值.
如图,直线l1和l2相交于点M,l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,|AM|=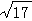 ,|AN|=3,且|BN|=6.建立适当的坐标系,求曲线段C的方程.(14分)
,|AN|=3,且|BN|=6.建立适当的坐标系,求曲线段C的方程.(14分)
河上有抛物线型拱桥,当水面距拱桥顶5米时,水面宽为8米,一小船宽4米,高2米,载货后船露出水面上的部分高0.75米,问水面上涨到与抛物线拱顶相距多少米时,小船开始不能通航?(12分)
动直线y =a,与抛物线 相交于A点,动点B的坐标是
相交于A点,动点B的坐标是 ,求线段AB中点M的轨迹的方程.(12分)
,求线段AB中点M的轨迹的方程.(12分)
已知抛物线的顶点在原点,对称轴是x轴,抛物线上的点M(-3,m)到焦点的距离等于5,求抛物线的方程和m的值.
已知动圆M与直线y =2相切,且与定圆C: 外切,求动圆圆心M的轨迹方程.(12分)
外切,求动圆圆心M的轨迹方程.(12分)