已知椭圆C: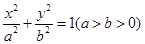 的离心率与双曲线
的离心率与双曲线 的离心率互为倒数,且以抛物线
的离心率互为倒数,且以抛物线 的焦点F为右焦点.
的焦点F为右焦点.
(1)求椭圆C的标准方程;
(2)过右焦点F作斜率为 的直线l交曲线C于M、N两点,且
的直线l交曲线C于M、N两点,且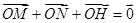 ,又点H关于原点O的对称点为点G,试问M、G、N、H四点是否共圆?若共圆,求出圆心坐标和半径;若不共圆,请说明理由.
,又点H关于原点O的对称点为点G,试问M、G、N、H四点是否共圆?若共圆,求出圆心坐标和半径;若不共圆,请说明理由.
数列{an}中,a1=8,a4=2且满足an+2=2an+1-an,(n∈N*).
(1)求数列{an}的通项公式;
(2)设Sn=|a1|+|a2|+…+|an|,求Sn;
(3)设bn=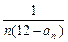 (n∈N*),Tn=b1+b2+……+bn(n∈N*),是否存在最大的整数m,使得对任意n∈N*均有Tn>
(n∈N*),Tn=b1+b2+……+bn(n∈N*),是否存在最大的整数m,使得对任意n∈N*均有Tn> 成立?若存在,求出m的值;若不存在,说明理由.
成立?若存在,求出m的值;若不存在,说明理由.
数列{an}满足a1=2,对于任意的n∈N*都有an>0,且(n+1)an2+an·an+1-nan+12=0,又知数列{bn}的通项为bn=2n-1+1.
(1)求数列{an}的通项an及它的前n项和Sn;
(2)求数列{bn}的前n项和Tn;
(3)猜想Sn与Tn的大小关系,并说明理由.
{an}为等差数列,公差d≠0,an≠0,(n∈N*),且akx2+2ak+1x+ak+2=0(k∈N*)
(1)求证:当k取不同自然数时,此方程有公共根;
(2)若方程不同的根依次为x1,x2,…,xn,…,
求证:数列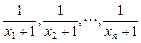 为等差数列.
为等差数列.
设{an}为等差数列,{bn}为等比数列,a1=b1=1,a2+a4=b3,b2·b4=a3,分别求出{an}及{bn}的前n项和S10及T10.
已知数列{an}为等差数列,公差d≠0,由{an}中的部分项组成的数列
a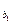 ,a
,a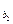 ,…,a
,…,a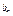 ,…为等比数列,其中b1=1,b2=5,b3=17.
,…为等比数列,其中b1=1,b2=5,b3=17.
(1)求数列{bn}的通项公式;
(2)记Tn=C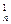 b1+C
b1+C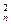 b2+C
b2+C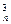 b3+…+C
b3+…+C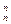 bn,求
bn,求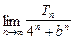 .
.