设函数 .
.
(1)讨论 的导函数
的导函数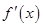 的零点的个数;
的零点的个数;
(2)证明:当
设命题 在区间
在区间 上是减函数;命题
上是减函数;命题
 是方程
是方程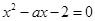 的两个实根,且不等式
的两个实根,且不等式 对任意的实数
对任意的实数 恒成立,若
恒成立,若 为真,试求实数
为真,试求实数 的取值范围.
的取值范围.
选做题(本小题满分10分)已知集合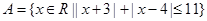 ,
, ,求集合
,求集合 .
.
(本小题满分12分)已知函数 (其中
(其中 ,
,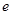 是自然对数的底数
是自然对数的底数
(1)若 ,判断函数
,判断函数 在区间
在区间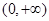 上的单调性;
上的单调性;
(2)若函数 有两个极值点
有两个极值点 ,
, ,求
,求 的取值范围;
的取值范围;
(3)在(2)的条件下,试证明: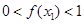 .
.
(本小题满分12分)若函数 是定义域
是定义域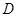 内的某个区间
内的某个区间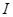 上的增函数,且
上的增函数,且 在
在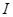 上是减函数,则称
上是减函数,则称 是I上的“非完美增函数”,已知
是I上的“非完美增函数”,已知 ,
, .
.
(1)判断 在
在 上是否是“非完美增函数”;
上是否是“非完美增函数”;
(2)若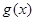 是
是 上的“非完美增函数”,求实数
上的“非完美增函数”,求实数 的取值范围.
的取值范围.
(本小题满分12分)在 中,角
中,角 所对的边分别是
所对的边分别是 ,若
,若 ,且
,且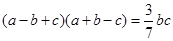 .
.
(1)求 的值;
的值;
(2)若 ,求
,求 的面积.
的面积.