已知函数 ,
, ,函数
,函数 的最小值为
的最小值为 .
.
(1)求 ;
;
(2)是否存在实数 、
、 同时满足以下条件:
同时满足以下条件:
① ;
;
②当 的定义域为
的定义域为 时,值域为
时,值域为 .若存在,求出
.若存在,求出 、
、 的值;若不存在,说明理由
的值;若不存在,说明理由
已知数列 的通项
的通项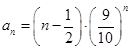 ,
,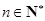 .
.
(Ⅰ)求 ;
;
(Ⅱ)判断数列 的增减性,并说明理由;
的增减性,并说明理由;
(Ⅲ)设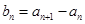 ,求数列
,求数列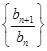 的最大项和最小项.
的最大项和最小项.
已知椭圆 两焦点坐标分别为
两焦点坐标分别为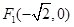 ,
,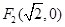 ,一个顶点为
,一个顶点为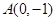 .
.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)是否存在斜率为 的直线
的直线 ,使直线
,使直线 与椭圆
与椭圆 交于不同的两点
交于不同的两点 ,满足
,满足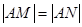 . 若存在,求出
. 若存在,求出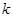 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
已知函数 ,其中
,其中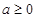 .
.
(Ⅰ)若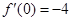 ,求
,求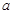 的值,并求此时曲线
的值,并求此时曲线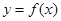 在点
在点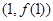 处的切线方程;
处的切线方程;
(Ⅱ)求函数 在区间
在区间 上的最小值.
上的最小值.
如图,在三棱锥 中,平面
中,平面 平面
平面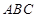 ,
, ,
, .设
.设 ,
, 分别为
分别为 ,
,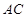 中点.
中点.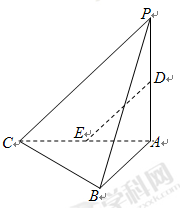
(Ⅰ)求证: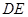 ∥平面
∥平面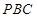 ;
;
(Ⅱ)求证: 平面
平面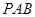 ;
;
(Ⅲ)试问在线段 上是否存在点
上是否存在点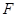 ,使得过三点
,使得过三点  ,
, ,
,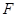 的平面内的任一条直线都与平面
的平面内的任一条直线都与平面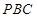 平行?若存在,指出点
平行?若存在,指出点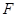 的位置并证明;若不存在,请说明理由.
的位置并证明;若不存在,请说明理由.
甲、乙两名同学参加“汉字听写大赛”选拔性测试.在相同的测试条件下,两人5次测试的成绩(单位:分)如下表:
(Ⅰ)请画出甲、乙两人成绩的茎叶图. 你认为选派谁参赛更好?说明理由(不用计算);
(Ⅱ)若从甲、乙两人5次的成绩中各随机抽取一个成绩进行分析,求抽到的两个成绩中至少有一个高于
90分的概率.