“水资源与永恒发展”是2015年联合国世界水资源日主题．近年来，某企业每年需要向自来水厂缴纳水费约4万元，为了缓解供水压力，决定安装一个可使用4年的自动污水净化设备，安装这种净水设备的成本费（单位：万元）与管线、主体装置的占地面积（单位：平方米）成正比，比例系数约为0．2．为了保证正常用水，安装后采用净水装置净水和自来水厂供水互补的用水模式．假设在此模式下，安装后该企业每年向自来水厂缴纳的水费 C（单位：万元）与安装的这种净水设备的占地面积x（单位：平方米）之间的函数关系是
（x≥0，k为常数）．记y为该企业安装这种净水设备的费用与该企业4年共将消耗的水费之和．
（1） 试解释 
的实际意义，请建立y关于x的函数关系式并化简;
（2） 当x为多少平方米时，y取得最小值？最小值是多少万元？
正三角形ABC的边长为1，且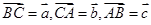
，求
的值。
已知向量
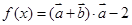，函数
求函数
的最小正周期T及值域
已知数列{an}，其前n项和为Sn.
(1)若对任意的n∈N，a2n－1，a2n＋1，a2n组成公差为4的等差数列，且a1＝1，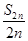
＝2013，求n的值；
(2)若数列
是公比为q(q≠－1)的等比数列，a为常数，求证：数列{an}为等比数列的充要条件为q＝1＋
.
设不等式组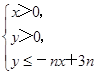
所表示的平面区域为Dn，记Dn内的整点个数为an(n∈N*)(整点即横坐标和纵坐标均为整数的点)．
(1)求数列{an}的通项公式；
(2)记数列{an}的前n项和为Sn，且Tn＝
.若对于一切的正整数n，总有Tn≤m，求实数m的取值范围．
已知数列{an}满足a1＋a2＋…＋an＝n2(n∈N*)．
(1)求数列{an}的通项公式；
(2)对任意给定的k∈N*，是否存在p，r∈N*(k<p<r)使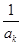
，
，
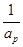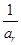成等差数列？若存在，用k分别表示p和r(只要写出一组)；若不存在，请说明理由．