某厂生产电子元件,其产品的次品率为5%,现从一批产品中的任意连续取出2件,求次品数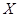 的概率分布
的概率分布
某一射手射击所得环数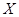 分布列为
分布列为
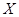 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
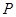 |
0.02 |
0.04 |
0.06 |
0.09 |
0.28 |
0.29 |
0.22 |
求此射手“射击一次命中环数≥7”的概率
一个类似于细胞分裂的物体,一次分裂为二,两次分裂为四,如此继续分裂有限多次,而随机终止.设分裂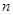 次终止的概率是
次终止的概率是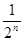 (
(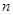 =1,2,3,…).记
=1,2,3,…).记 为原物体在分裂终止后所生成的子块数目,求
为原物体在分裂终止后所生成的子块数目,求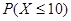 .
.
一盒中放有大小相同的红色、绿色、黄色三种小球,已知红球个数是绿球个数的两倍,黄球个数是绿球个数的一半.现从该盒中随机取出一个球,若取出红球得1分,取出黄球得0分,取出绿球得-1分,试写出从该盒中取出一球所得分数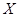 的分布列.
的分布列.
某城市出租汽车的起步价为10元,行驶路程不超出4km,则按10元的标准收租车费若行驶路程超出4km,则按每超出lkm加收2元计费(超出不足1km的部分按lkm计).从这个城市的民航机场到某宾馆的路程为15km.某司机常驾车在机场与此宾馆之间接送旅客,由于行车路线的不同以及途中停车时间要转换成行车路程(这个城市规定,每停车5分钟按lkm路程计费),这个司机一次接送旅客的行车路程ξ是一个随机变量,他收旅客的租车费可也是一个随机变量
(1)求租车费η关于行车路程ξ的关系式;
(2)已知某旅客实付租车费38元,而出租汽车实际行驶了15km,问出租车在途中因故停车累计最多几分钟?