某城市出租汽车的起步价为10元,行驶路程不超出4km,则按10元的标准收租车费若行驶路程超出4km,则按每超出lkm加收2元计费(超出不足1km的部分按lkm计).从这个城市的民航机场到某宾馆的路程为15km.某司机常驾车在机场与此宾馆之间接送旅客,由于行车路线的不同以及途中停车时间要转换成行车路程(这个城市规定,每停车5分钟按lkm路程计费),这个司机一次接送旅客的行车路程ξ是一个随机变量,他收旅客的租车费可也是一个随机变量
(1)求租车费η关于行车路程ξ的关系式;
(2)已知某旅客实付租车费38元,而出租汽车实际行驶了15km,问出租车在途中因故停车累计最多几分钟?
选修4—1:几何证明选讲
如图,设△ABC的外接圆的切线AE与BC的延长线交于点E,∠BAC的平分线与BC交于点D.求证:

(本小题满分12分)已知过点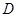
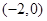 的直线
的直线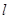 与椭圆
与椭圆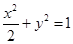 交于不同的两点
交于不同的两点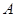 、
、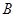 ,点
,点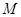 是弦
是弦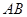 的中点.
的中点.
(Ⅰ)若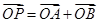 ,求点
,求点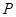 的轨迹方程;
的轨迹方程;
(Ⅱ)求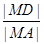 的取值范围.
的取值范围.
(本小题满分12分)已知函数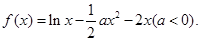
(1)若函数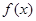 在定义域内单调递增,求
在定义域内单调递增,求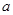 的取值范围;
的取值范围;
(2)若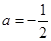 且关于x的方程
且关于x的方程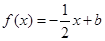 在
在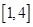 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数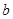 的取值范围;
的取值范围;
(本小题满分12分)在四棱锥 中,
中, 平面
平面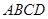 ,底面
,底面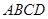 为矩形,
为矩形,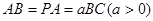 .
.
(Ⅰ)当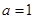 时,求证:
时,求证: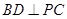 ;
;
(Ⅱ)若 边上有且只有一个点
边上有且只有一个点 ,使得
,使得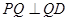 ,求此时二面角
,求此时二面角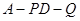 的余弦值.
的余弦值.
(本小题满分12分)
某地区对12岁儿童瞬时记忆能力进行调查.瞬时记忆能力包括听觉记忆能力与视觉记忆能力.某班学生共有40人,下表为该班学生瞬时记忆能力的调查结果.例如表中听觉记忆能力为中等,且视觉记忆能力偏高的学生为3人.
 视觉 视觉 |
视觉记忆能力 |
||||
| 偏低 |
中等 |
偏高 |
超常 |
||
| 听觉 记忆 能力 |
偏低 |
0 |
7 |
5 |
1 |
| 中等 |
1 |
8 |
3 |
 |
|
| 偏高 |
2 |
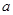 |
0 |
1 |
|
| 超常 |
0 |
2 |
1 |
1 |
由于部分数据丢失,只知道从这40位学生中随机抽取一个,视觉记忆能力恰为中等,且听觉记忆能力为中等或中等以上的概率为 .
.
(I)试确定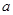 、
、 的值;
的值;
(II)从40人中任意抽取3人,求其中至少有一位具有听觉记忆能力或视觉记忆能力超常的学生的概率;
(III)从40人中任意抽取3人,设具有听觉记忆能力或视觉记忆能力偏高或超常的学生人数为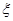 ,求随机变量
,求随机变量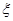 的数学期望
的数学期望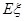 .
.