如图,在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.
(1)试判定△ODE的形状,并说明你的理由;
(2)线段BD、DE、EC三者之间有什么数量关系?写出你的判断过程.
解方程:
把2014个正整数1,2,3,4,…,2015按如图方式排列成一个表.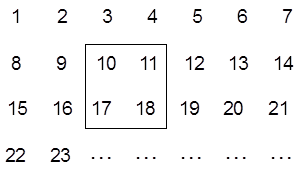
(1)如上图,用一正方形框在表中任意框住4个数,记左上角的一个数为x,则另三个数用含x的式子表示出来,从小到大依次是___________,____________,____________.
(2)当(1)中被框住的4个数之和等于416时,x的值为多少?
(3)在(1)中能否框住这样的4个数,它们的和等于324?若能,则求出x的值;若不能,则说明理由.
书正和子轩两人登一座山,书正每分钟登高10米,并且先出发30分钟,子轩每分钟登高15米,两人同时登上山顶.
(1)这座山有多高?
(2)如果将题中“书正先出发30分钟”这个条件改为“书正先爬山200米”其他条件不变,问子轩出发多少分钟追上书正?
某车间有22名工人生产螺钉和螺母,每人每天平均生产螺钉1200或螺母2000个,一个螺钉要配两个螺母;为了使每天生产的产品正好配套,应该如何安排工人生产 ?
吕洁要把一些图书分给某班同学阅读,如果每人3本,则剩余40本;若每人4本,则还缺少25本,(1)这个班级有多少人?(2)总共有多少本书?