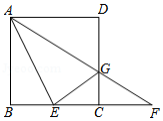
如图,在正方形 中,点 在 边上,连接 , 的平分线 与 边交于点 ,与 的延长线交于点 .设 .
(1)若 , ,求线段 的长.
(2)连接 ,若 ,
①求证:点 为 边的中点.
②求 的值.
设函数 , .
(1)当 时,函数 的最大值是 ,函数 的最小值是 ,求 和 的值.
(2)设 ,且 ,当 时, ;当 时, .圆圆说:“ 一定大于 ”.你认为圆圆的说法正确吗?为什么?
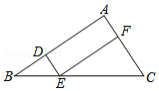
如图,在 中,点 , , 分别在 , , 边上, , .
(1)求证: .
(2)设 ,
①若 ,求线段 的长;
②若 的面积是20,求 的面积.
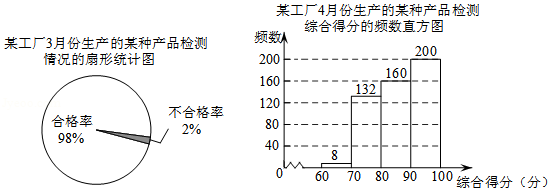
某工厂生产某种产品,3月份的产量为5000件,4月份的产量为10000件.用简单随机抽样的方法分别抽取这两个月生产的该产品若干件进行检测,并将检测结果分别绘制成如图所示的扇形统计图和频数直方图(每组不含前一个边界值,含后一个边界值).已知检测综合得分大于70分的产品为合格产品.
(1)求4月份生产的该产品抽样检测的合格率;
(2)在3月份和4月份生产的产品中,估计哪个月的不合格件数多?为什么?
以下是圆圆解方程 的答案过程.
解:去分母,得 .
去括号,得 .
移项,合并同类项,得 .
圆圆的答案过程是否有错误?如果有错误,写出正确的答案过程.