如图,梯形ABCD中,AB//CD,且AB=2CD,E,F分别是AB,BC的中点.
EF与BD相交于点M.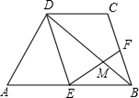
(1)求证:△EDM∽△FBM;
(2)若DB=9,求BM.
某市政府计划修建一处公共服务设施,使它到三所公寓A、B、C 的距离相等。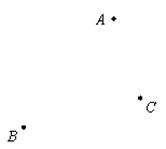
若三所公寓A、B、C的位置如图所示,请你在图中确定这处公共服务设施(用点P表示)的位置(尺规作图,保留作图痕迹,不写作法);
若∠BAC=56º,则∠BPC= º.
如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:(用直尺画图)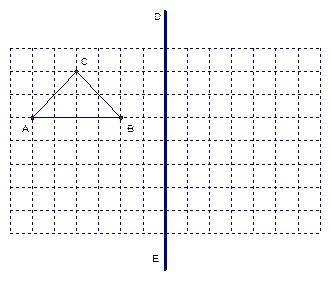
画出格点△ABC(顶点均在格点上)关于直线DE对称的△A1B1C1;
在DE上画出点P,使
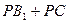 最小
最小在DE上画出点Q,使
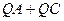 最小
最小
半径为5的⊙O中,直径AB的不同侧有定点C和动点P. 已知BC∶CA=4∶3,点P在弧AB上运动,过点C作CP的垂线,与PB的延长线交于点Q. 求证:△ABC∽△PQC;
当点P与点C关于AB对称时,求CQ的长;
当点P运动到什么位置时,CQ取到最大值?求此时CQ的长;
当点P运动到弧AB的中点时,求CQ的长.

直线y=-x+6与坐标轴分别交于A、B两点,动点P、Q同时从O点匀速出发,同时到达A点时运动停止.点Q沿线段OA运动,速度为每秒1个单位长度,点P沿路线O→B→A运动.
直接写出A、B两点的坐标;
设点Q的运动时间为t秒,△OPQ的面积为S,求出S与t之间的函数关系式;
当s= 时,求出点P的坐标,并直接写出以点O、P、Q为顶点的平行四边形的
第四个顶点M的坐标.
在△ABC中, AB、BC、AC三边的长分别为、、,求这个三角形的面积.小华同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.这种方法叫做构图法.△ABC的面积为:.
若△DEF三边的长分别为、2、,请在图2的正方形网格中画出相应的△DEF,并利用构图法求出它的面积.


利用第2小题解题方法完成下题:如图3,一个六边形的花坛被分割成7个部分,其中正方形PRBA,RQDC,QPFE的面积分别为13、10、17,且△PQR、△BCR、△DEQ、△AFP的面积相等,求六边形花坛ABCDEF的面积.
