在“文化南长•全民阅读”活动中,某中学社团“清风读书社”对全校学生的人数及纸质图书阅读量(单位:本)进行了调查.2014年全校有1000名学生,2015年全校学生人数比2014年增加10%,2016年全校学生人数比2015年增加100人.
(1)2016年全校学生有 人;
(2)2015年全校学生人均阅读量比2014年多1本,阅读总量比2014年增加1700本.
(注:阅读总量=人均阅读量×人数)
①求2014年全校学生人均阅读量;
②2014年读书社人均阅读量是全校学生人均阅读量的2.5倍,如果2015年、2016年这两年读书社人均阅读量都比前一年增长一个相同的百分数a,2016年全校学生人均阅读量比2014年增加的百分数也是a,那么2016年读书社全部80名成员的阅读总量将达到全校学生阅读总量的25%,求a的值.
(本题10分)如图,AB∥CD,E是AB上一点,DE交AC于点F,AE=CD,分别延长DE和
CB交于点G.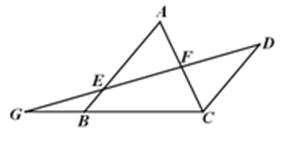
(1)求证:△AEF≌△CDF;
(2)若GB=2,BC=4,BE=1,求AB的长.
(本题8分)如图是由边长都是1的小正方形组成的网格.请以图中线段BC为边,作△PBC,
使P在格点上,并满足: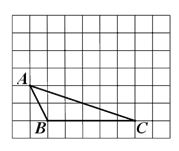


(1)图甲中的△PBC是直角三角形,且面积是△ABC面积2倍;
(2)图乙中的△PBC是等腰非直角三角形.
(本题10分)
(1)计算: 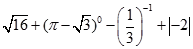 .
.
(2)解方程: .
.
(本题满分14分)抛物线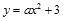 交
交 轴于A(-4,0)、B两点,交
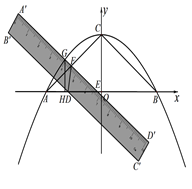
轴于A(-4,0)、B两点,交 轴于C.将一把宽度为1.2的直尺如图放置在直角坐标系中,使直尺边
轴于C.将一把宽度为1.2的直尺如图放置在直角坐标系中,使直尺边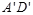 ∥
∥ ,直尺边
,直尺边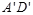 交
交 轴于E,交AC于F,交抛物线于G,直尺另一边
轴于E,交AC于F,交抛物线于G,直尺另一边 交
交 轴于D.当点D与点A重合时,把直尺沿
轴于D.当点D与点A重合时,把直尺沿 轴向右平移,当点E与点B重合时,停止平移,在平移过程中,△FDE的面积为S.
轴向右平移,当点E与点B重合时,停止平移,在平移过程中,△FDE的面积为S.
(1)请你求出抛物线解析式及S的最大值;
(2)在直尺平移过程中,直尺边 上是否存在一点P,使点
上是否存在一点P,使点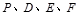 构成的四边形是这菱形,若
构成的四边形是这菱形,若
存在,请你求出点P坐标;若不存在,请说明理由;
(3)过G作GH⊥ 轴于H
轴于H
① 在直尺平移过程中,请你求出GH+HO的最大值;
②点Q、R分别是HC、HB的中点,请你直接写出在直尺平移过程中,线段QR扫过的图形的周长.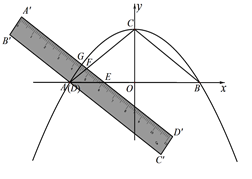
温州某绿色无公害蔬菜基地有甲、乙两种植户,他们种植了A、B两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如下表:
| 种植户 |
种植A类蔬菜面积 (单位:亩) |
种植B类蔬菜面积 (单位:亩) |
总收入 (单位:元) |
每亩成本(单位:元) |
| 甲 |
3 |
1 |
12500 |
1400 |
| 乙 |
2 |
3 |
16500 |
1600 |
说明:不同种植户种植的同类蔬菜每亩平均收入相等.
⑴求A、B两类蔬菜每亩平均收入各是多少元?
⑵某种植户准备租20亩地用来种植A、B两类蔬菜,为了使总收入不低于63000元,且种植A类蔬菜的面积多于种植B类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户的最大利润方案.