某检修小组从A地出发，在东西向的马路上检修线路，如果规定向东行驶为正，向西行驶为负，一天中七次行驶记录如下．（单位：km）
| 第一次 |
第二次 |
第三次 |
第四次 |
第五次 |
第六次 |
第七次 |
| －4 |
＋7 |
－9 |
＋10 |
＋6 |
－5 |
－6 |
（1）求收工时，检修小组在A地的哪个方向？距离A地多远？
（2）在第几次记录时距A地最近？
（3）若汽车行驶每千米耗油0．2升，问从A地出发，检修结束后再回到A地共耗油多少升？
五边形ABCDE中，∠EAB=∠ABC=∠BCD=90°，AB=BC，且满足以点B为圆心，AB长为半径的圆弧AC与边DE相切于点F，连接BE，BD．
（1）如图1，求∠EBD的度数；
（2）如图2，连接AC，分别与BE，BD相交于点G，H，若AB=1，∠DBC=15°，求AG•HC的值．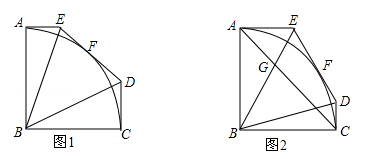
如图，AC是⊙O的直径，点B在⊙O上，∠ACB=30°．
（1）利用尺规作∠ABC的平分线BD，交AC于点E，交⊙O于点D，连接CD（保留作图痕迹，不写作法）；
（2）在（1）所作的图形中，求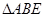
与
的面积之比．
如图1，水平放置一个三角板和一个量角器，三角板的边AB和量角器的直径DE在一条直线上，AB=BC=6cm，OD=3cm开始的时候BD=1cm,现在三角板以2cm/s的速度向右移动。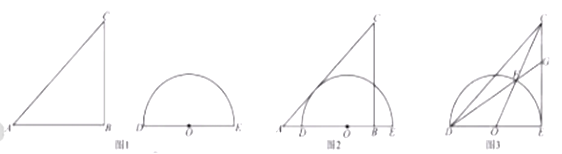
（1）当B与O重合的时候，求三角板运动的时间；
（2）如图2，当AC与半圆相切时，求AD；
（3）如图3，当AB和DE重合时，求证：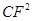
=CG·CE．
⊙O是△ABC的外接圆，AB是直径，过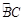
的中点P作⊙O的直径PG交弦BC于点D，连接AG， CP，PB．
（1）如1图；若D是线段OP的中点，求∠BAC的度数；
（2）如2图，在DG上取一点k，使DK=DP，连接CK，求证：四边形AGKC是平行四边形；
（3）如3图；取CP的中点E，连接ED并延长ED交AB于点H，连接PH，求证：PH⊥AB．
如图，在平行四边形ABCD中，AB＜BC．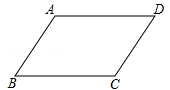
（1）利用尺规作图，在BC边上确定点E，使点E到边AB，AD的距离相等（不写作法，保留作图痕迹）；
（2）若BC=8，CD=5，则CE= ．