已知圆C: .
.
(1)写出圆C的标准方程,并指出圆心坐标和半径大小 ;
(2)是否存在斜率为1的直线m,使m被圆C截得的弦为AB,且 (O为坐标原点).若存在,求出直线m的方程;若不存在,说明理由.
(O为坐标原点).若存在,求出直线m的方程;若不存在,说明理由.
(本小题满分12分)
在△ABC中,内角A,B,C所对边长分别为 ,
, ,
, ,
, .
.
(Ⅰ)求 的最大值及
的最大值及 的取值范围;
的取值范围;
(Ⅱ)求函数 的最值.
的最值.
(本小题满分12分)
设函数 曲线y=f(x)通过点(0,2a+3),且
曲线y=f(x)通过点(0,2a+3),且
在点(-1,f(-1))处的切线垂直于y轴.
(Ⅰ)用a分别表示b和c;
(Ⅱ)当bc取得最小值时,求函数g(x)=-f(x)e-x的单调区间.
(本小题满分10分)
已知曲线y=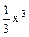 在x=x0处的切线L经过点P(2,
在x=x0处的切线L经过点P(2, ),求切线L的方程。
),求切线L的方程。
(本小题满分12分)
已知双曲线过点P ,它的
,它的 渐近线方程为
渐近线方程为
(1)求双曲线的标准方程;
(2)设F1和F2是这双曲线的左、右焦点,点P在这双曲线上,且|PF1|·|PF2|=32,求∠F1PF2的大小.
(本小题12分)
抛物线 上有两个定点A、B分别在对称轴的上、下两侧,F为抛物线的焦点,并且|FA|=2,|FB|=5,(1)求直线AB的方程。
上有两个定点A、B分别在对称轴的上、下两侧,F为抛物线的焦点,并且|FA|=2,|FB|=5,(1)求直线AB的方程。
(2)在抛物线AOB这段曲线上求一点P,使△PAB的面积最大,并求这个最大面积.