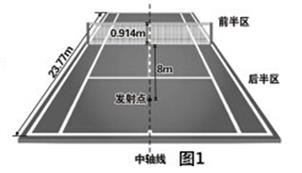
小明同学制作了一个简易的网球发射器,可用于帮忙练习定点接发球,如图1所示,网球场前半区、后半区总长为23.77米,球网的中间部分高度为0.914米,发射器固定安装在后半区离球网底部8米处中轴线上,发射方向与球网底部所在直线垂直.为计算方便,球场长度和球网中间高度分别按24米和1米计算,发射器和网球大小均忽略不计.如图2所示,以发射器所在位置为坐标原点建立平面直角坐标系 ,
, 轴在地平面上的球场中轴线上,
轴在地平面上的球场中轴线上,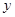 轴垂直于地平面,单位长度为1米.已知若不考虑球网的影响,网球发射后的轨迹在方程
轴垂直于地平面,单位长度为1米.已知若不考虑球网的影响,网球发射后的轨迹在方程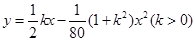 表示的曲线上,其中
表示的曲线上,其中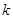 与发射方向有关.发射器的射程是指网球落地点的横坐标.
与发射方向有关.发射器的射程是指网球落地点的横坐标.
(1)求发射器的最大射程;
(2)请计算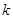 在什么范围内,发射器能将球发过网(即网球飞行到球网正上空时,网球离地距离大于1米)?若发射器将网球发过球网后,在网球着地前,小明要想在前半区中轴线的正上空选择一个离地面2.55米处的击球点正好击中网球,试问击球点的横坐标
在什么范围内,发射器能将球发过网(即网球飞行到球网正上空时,网球离地距离大于1米)?若发射器将网球发过球网后,在网球着地前,小明要想在前半区中轴线的正上空选择一个离地面2.55米处的击球点正好击中网球,试问击球点的横坐标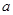 最大为多少?并请说明理由.
最大为多少?并请说明理由.
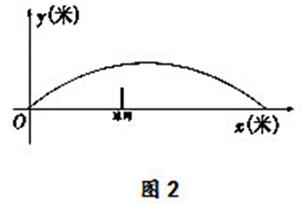
如图,已知椭圆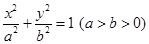 过点
过点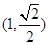 ,离心率为
,离心率为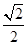 ,左、右焦点分别为
,左、右焦点分别为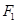 、
、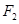 .点
.点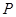 为直线
为直线 上且不在
上且不在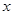 轴上的任意一点,直线
轴上的任意一点,直线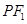 和
和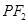 与椭圆的交点分别为
与椭圆的交点分别为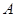 、
、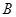 和
和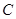 、
、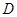 ,
,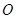 为坐标原点.设直线
为坐标原点.设直线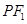 、
、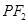 的斜率分别为
的斜率分别为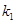 、
、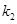 .
.
(i)证明: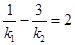 ;
;
(ii)问直线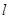 上是否存在点
上是否存在点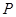 ,使得直线
,使得直线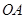 、
、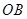 、
、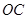 、
、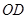 的斜率
的斜率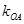 、
、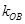 、
、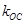 、
、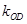 满足
满足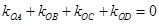 ?若存在,求出所有满足条件的点
?若存在,求出所有满足条件的点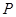 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
已知函数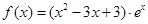 .
.
(1)求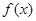 的单调区间;
的单调区间;
(2)当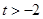 时,判断
时,判断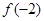 和
和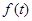 的大小,并说明理由;
的大小,并说明理由;
(3)求证:当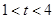 时,关于
时,关于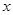 的方程:
的方程: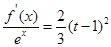 在区间
在区间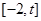 上总有两个不同的解.
上总有两个不同的解.
已知椭圆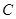 的中心在原点,焦点在
的中心在原点,焦点在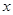 轴上.若椭圆上的点
轴上.若椭圆上的点 到焦点
到焦点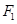 、
、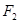 的距离之和等于4.
的距离之和等于4.
(1)写出椭圆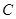 的方程和焦点坐标.
的方程和焦点坐标.
(2)过点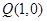 的直线与椭圆交于两点
的直线与椭圆交于两点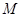 、
、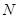 ,当
,当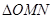 的面积取得最大值时,求直线
的面积取得最大值时,求直线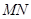 的方程.
的方程.
如图,矩形 中,
中,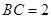 ,
,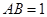 ,
,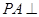 平面
平面 ,
,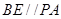 ,
, ,
,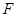 为
为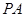 的中点.
的中点.
(1)求证: 平面
平面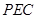 .
.
(2)若 ,求平面
,求平面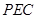 与平面
与平面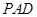 所成锐二面角的余弦值.
所成锐二面角的余弦值.
甲、乙、丙三人独立破译同一份密码,已知甲、乙、丙各自破译出密码的概率分别为 、
、 、
、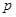 ,且他们是否破译出密码互不影响,若三人中只有甲破译出密码的概率为
,且他们是否破译出密码互不影响,若三人中只有甲破译出密码的概率为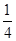 .
.
(1)求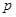 的值.
的值.
(2)设甲、乙、丙三人中破译出密码的人数为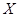 ,求
,求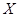 的分布列和数学期望
的分布列和数学期望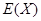 .
.