已知等差数列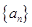 的首项
的首项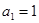 ,公差
,公差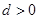 ,且
,且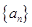 的第二项、第五项、第十四项成等比数列。
的第二项、第五项、第十四项成等比数列。
(1)求数列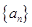 的通项公式;
的通项公式;
(2)设 ,记
,记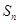 为数列
为数列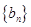 的前n项和,求
的前n项和,求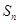 并说明是否存在最大的整数t,使得对任意的n均有
并说明是否存在最大的整数t,使得对任意的n均有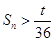 总成立?若存在,求出t;若不存在,请说明理由.
总成立?若存在,求出t;若不存在,请说明理由.
设椭圆 的左右焦点分别为 ,离心率 ,右准线为 是 上的两个动点, 。
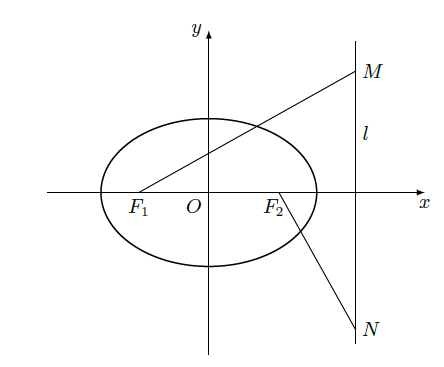
(Ⅰ)若
,求
的值;
(Ⅱ)证明:当
取最小值时,
与
共线。
如图,平面
平面
,四边形
与
都是直角梯形,
,
,
。
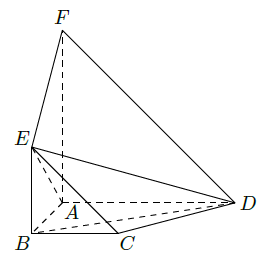
(Ⅰ)证明:
四点共面;
(Ⅱ)设
,求二面角
的大小。
设进入某商场的每一位顾客购买甲种商品的概率为
,购买乙种商品的概率为
,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的。
(Ⅰ)求进入商场的1位顾客购买甲、乙两种商品中的一种的概率;
(Ⅱ)求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率;
(Ⅲ)记 表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求
的分布列及期望。
表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求
的分布列及期望。
(本小题满分12分)
设函数f(x)=ax+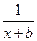 (a,b∈Z),曲线y=f(x)在点(2,f(2))处的切线方程为y=3。
(a,b∈Z),曲线y=f(x)在点(2,f(2))处的切线方程为y=3。
(Ⅰ)求f(x)的解析式:
(Ⅱ)证明:函数y=f(x)的图像是一个中心对称图形,并求其对称中心;
(Ⅲ)证明:曲线y=f(x)上任一点的切线与直线x=1和直线y=x所围三角形的面积为定值,并求出此定值。
、
两个投资项目的利润率分别为随机变量
和
.根据市场分析,
,
的分布列分别为
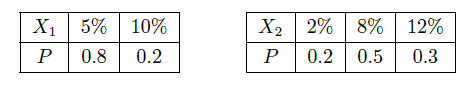
(Ⅰ)在
、
两个项目上各投资
万元,
和
分别表示投资项目
和
所获得的利润,求方差
,
;
(Ⅱ)将
万元投资A项目,
万元投资
项目,
表示投资
项目所得利润的方差与投资
项目所得到利润的方差的和。求
的最小值,并指出
为何值时,
取到最小值。
(注:
)