将圆x2＋y2＝1上每一点的横坐标保持不变，纵坐标变为原来的2倍，得曲线C．
（1）写出C的参数方程；
（2）设直线l：2x＋y－2＝0与C的交点为P1，P2，以坐标原点为极点，x轴正半轴为极轴建立极坐标系，求过线段P1P2的中点且与l垂直的直线的极坐标方程．
已知圆C经过A（1，1）、B（2，
）两点，且圆心C在直线l：x-y+1=0上，求圆C的标准方程.
已知半径为
的球内有一个内接正方体（即正方体的顶点都在球面上）.
（1）求此球的体积；
（2）求此球的内接正方体的体积；
（3）求此球的表面积与其内接正方体的全面积之比.
已知函数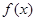
满足：对任意
，都有
成立，且
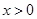时，
．
（1）求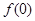
的值，并证明：当
时，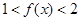
；
（2）判断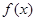的单调性并加以证明；
（3）若
在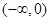
上递减，求实数
的取值范围．
设函数
(
)．
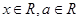（1）若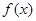
为偶函数，求实数
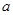的值；
（2）已知
，若对任意
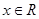都有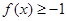
恒成立，求实数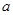的取值范围．
某自来水厂的蓄水池存有400吨水，水厂每小时可向蓄水池中注水60吨，同时蓄水池又向居民小区不间断供水，
小时内供水总量为
吨（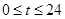
），从供水开始到第几小时时，蓄水池中的存水量最少？最少水量是多少吨？