在“斜面沙壶”的游戏中，要求游戏者通过一光滑的斜面将质量为m的物块送上高处的水平传送带后运送到网兜内．斜面长度为
，倾角为θ=30°，传送带距地面高度为，传送带的长度为3.传送带表面的动摩擦因数μ=0.5，传送带一直以速度
顺时针运动.当游戏者第一次试操作时，瞬间给予小物块一初速度v1（未知），只能将物块刚好送到斜面顶端；第二次调整初速度，恰好让物块水平冲上传送带.求：
（1）第一次小物块瞬间获得的初速度v1；
（2）第二次小物块滑上传送带的速度v2和传送带距斜面顶端的水平距离s；
（3）第二次小物块通过传送带过程中摩擦力对物块所做功以及系统产生的热量。
如图所示，一小球从倾角θ的斜坡顶端的A点，以初速υ0 水平抛出，落到斜坡上的B点，则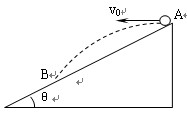
（1）小球从A到B的运动时间为；
（2）从A点抛出后经时间小球离斜面最远。
如图甲所示．竖直放置的金属板A、B中间开有小孔，小孔的连线沿水平放置的金属板C、D的中间线．粒子源P可以连续地产生质量为m、电荷量为q的带正电粒子（初速不计），粒子在A、B间被加速后。再进入金屑板C、D间偏转并均能从此电场中射出．已知金属板A、B间电压为U0，金属板C、D间电压为
。C、D板长度均为L，间距
为
，在金属板C、D右侧有如图乙所示的匀强磁场，其中
，（磁场变化周期未知），粒子重力不计．
（1）求粒子离开偏转电场时的速度大小；
（2）设垂直纸面向里的磁场方向为正方向，
时刻粒子进入磁场，
时刻该粒子的速度方向恰好竖直向上，求该粒子从射人磁场到离开磁场的总时间
。
如图所示，质量为M且足够长的木板放在光滑水平面上，其右端有一质量为m、可视为质点的滑块，滑块与木板问的动摩擦因数为μ。劲度系数为
的水平轻弹簧的右端O固定不动，其自由端A与滑块的距离为L。现给木板一水平向右的瞬时速度
，滑块将由静止开始向右运动，与弹簧接触后经过一段时间向右运动的速度到达最大，且滑块的速度始终小于木板的速度（弹簧在形变在弹性限度内，重力加速度大小为g，不计空气阻力）求：
（1）滑块刚接触弹
簧对滑块的速度大小v1和木板的速度大小
（2）滑块向右运动的速度到达最大值的过程中，弹簧的压缩量
及弹簧对滑块所做的功W（已知弹簧对滑块所做的功可用公式
计算，其中表示弹簧被压缩的长度）
（3）滑块向右运动的最大速度
。
如图．一根光滑绝缘细杆与水平面成
的角倾斜固定放置，细杆的一部分处在场强方向水平向右的匀强电场中，场强E=2×l04N／C在细杆上套有一个带电量为
C、质量为m=3×l0-2kg的小球．现使小球从细秆的顶端A处由静止开始沿杆滑下。并从B点进入电场。小球在电场中滑至最远处的C点。已知AB间的距离
。求：
（1）带电小球在B点的速度；
（2）带电小球进入电场后滑行的最大距离；
（3）带电小球A点滑至C点的时间。
如左图所示，空间存在着竖直向下的B=0.5T的匀强磁场，MN、PQ是放在同一水平面的光滑平行长直导轨，其间距L=0.2m，R是连接在导轨一端的电阻，ab是跨接在导轨上的导体棒，从零时刻开始，对a b加以大小为F=0.45N，方向水平向左的水平拉力，使其从静止开始沿导轨运动，此过程中，棒一直保持与导轨垂直且良好接触，右图是导体棒的速度时间图象，其中AO是图象在O点的切线，AB是图象的渐近线。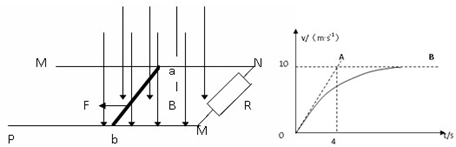
（1）除R以外，其余部分电阻均不计，求R的阻值。
（2）当ab位移100m时，其速度刚好到达10m/s，求此过程中电阻R上产生的热量