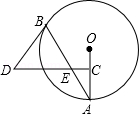
如图,△ABC内接于⊙O,AD⊥BC,OE⊥BC,OE= BC.
BC.
(1)求∠BAC的度数.
(2)将△ACD沿AC折叠为△ACF,将△ABD沿AB折叠为△ABG,延长FC和GB相交于点H.求证:四边形AFHG是正方形.
(3)若BD=6,CD=4,求AD的长.
解方程:
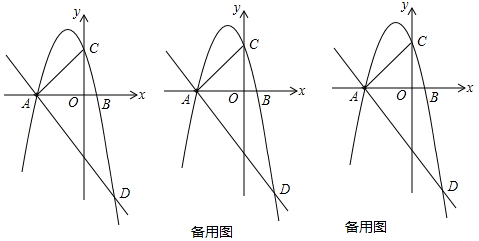
如图所示,已知抛物线 ,与x轴从左至右依次相交于A、B两点,与y轴相交于点C,经过点A的直线 与抛物线的另一个交点为D.
(1)若点D的横坐标为2,求抛物线的函数解析式;
(2)若在第三象限内的抛物线上有点P,使得以A、B、P为顶点的三角形与△ABC相似,求点P的坐标;
(3)在(1)的条件下,设点E是线段AD上的一点(不含端点),连接BE.一动点Q从点B出发,沿线段BE以每秒1个单位的速度运动到点E,再沿线段ED以每秒 个单位的速度运动到点D后停止,问当点E的坐标是多少时,点Q在整个运动过程中所用时间最少?
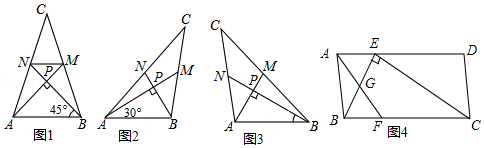
爱好思考的小茜在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线互相垂直的三角形称为“中垂三角形”.如图(1)、图(2)、图(3)中,AM、BN是△ABC的中线, 于点P,像△ABC这样的三角形均为“中垂三角形”.设 .
【特例探究】
(1)如图1,当 , 时,a= ,b= ;
如图2,当 , 时,a= ,b= ;
【归纳证明】
(2)请你观察(1)中的计算结果,猜想a2、b2、c2三者之间的关系,用等式表示出来,并利用图3证明你的结论.
【拓展证明】
(3)如图4,▱ABCD中,E、F分别是AD、BC的三等分点,且 ,连接AF、BE、CE,且 于E,AF与BE相交点G, , ,求AF的长.
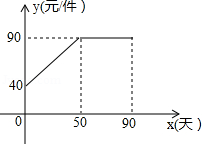
九年级(3)班数学兴趣小组经过市场调查整理出某种商品在第x天( ,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元).
|
时间x(天) |
1 |
30 |
60 |
90 |
|
每天销售量p(件) |
198 |
140 |
80 |
20 |
(1)求出w与x的函数关系式;
(2)问销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?请直接写出结果.
如图,AB是⊙O的弦,点C为半径OA的中点,过点C作 交弦AB于点E,连接BD,且 .
(1)判断BD与⊙O的位置关系,并说明理由;
(2)若 , ,求⊙O的直径.