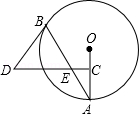
如图,AB是⊙O的弦,点C为半径OA的中点,过点C作 交弦AB于点E,连接BD,且 .
(1)判断BD与⊙O的位置关系,并说明理由;
(2)若 , ,求⊙O的直径.
近年来,我市大力发展城市快速交通,小王开车从家到单位有两条路线可选择,路线 为全程 的普通道路,路线 包含快速通道,全程 ,走路线 比走路线 平均速度提高 ,时间节省 ,求走路线 的平均速度.
一只不透明袋子中装有1个白球和若干个红球,这些球除颜色外都相同,某课外学习小组做摸球试验:将球搅匀后从中任意摸出1个球,记下颜色后放回、搅匀,不断重复这个过程,获得数据如下:
|
摸球的次数 |
200 |
300 |
400 |
1000 |
1600 |
2000 |
|
摸到白球的频数 |
72 |
93 |
130 |
334 |
532 |
667 |
|
摸到白球的频率 |
0.3600 |
0.3100 |
0.3250 |
0.3340 |
0.3325 |
0.3335 |
(1)该学习小组发现,摸到白球的频率在一个常数附近摆动,这个常数是 .(精确到 ,由此估出红球有 个.
(2)现从该袋中摸出2个球,请用树状图或列表的方法列出所有等可能的结果,并求恰好摸到1个白球,1个红球的概率.
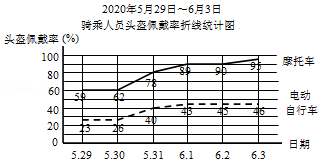
2020年6月1日起,公安部在全国开展"一盔一带"安全守护行动.某校小交警社团在交警带领下,从5月29日起连续6天,在同一时段对某地区一路口的摩托车和电动自行车骑乘人员佩戴头盔情况进行了调查,并将数据绘制成如下图表:
2020年6月2日骑乘人员头盔佩戴情况统计表
|
骑乘摩托车 |
骑乘电动自行车 |
|
|
戴头盔人数 |
18 |
72 |
|
不戴头盔人数 |
2 |
|
(1)根据以上信息,小明认为6月3日该地区全天摩托车骑乘人员头盔佩戴率约为 .你是否同意他的观点?请说明理由;
(2)相比较而言,你认为需要对哪类人员加大宣传引导力度?为什么?
(3)求统计表中 的值.
(1)计算: ;
(2)解不等式组:
如图,已知 , 是 的平分线, 是射线 上一点, .动点 从点 出发,以 的速度沿 水平向左作匀速运动,与此同时,动点 从点 出发,也以 的速度沿 竖直向上作匀速运动.连接 ,交 于点 .经过 、 、 三点作圆,交 于点 ,连接 、 .设运动时间为 ,其中 .
(1)求 的值;
(2)是否存在实数 ,使得线段 的长度最大?若存在,求出 的值;若不存在,说明理由.
(3)求四边形 的面积.
