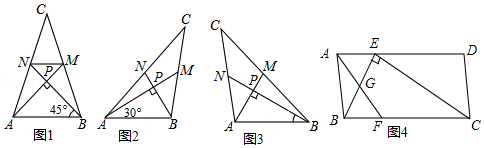
爱好思考的小茜在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线互相垂直的三角形称为“中垂三角形”.如图(1)、图(2)、图(3)中,AM、BN是△ABC的中线, 于点P,像△ABC这样的三角形均为“中垂三角形”.设 .
【特例探究】
(1)如图1,当 , 时,a= ,b= ;
如图2,当 , 时,a= ,b= ;
【归纳证明】
(2)请你观察(1)中的计算结果,猜想a2、b2、c2三者之间的关系,用等式表示出来,并利用图3证明你的结论.
【拓展证明】
(3)如图4,▱ABCD中,E、F分别是AD、BC的三等分点,且 ,连接AF、BE、CE,且 于E,AF与BE相交点G, , ,求AF的长.
如图,在直角坐标系xOy中,正方形OCBA的顶点A,C分别在y轴,x轴上,点B坐标为(6,6),抛物线y=ax2+bx+c经过点A,B两点,且3a-b=-1.
(1)求a,b,c的值;
(2)如果动点E,F同时分别从点A,点B出发,分别沿A→B,B→C运动,速度都是每秒1个单位长度,当点E到达终点B时,点E,F随之停止运动,设运动时间为t秒,△EBF的面积为S.
①试求出S与t之间的函数关系式,并求出S的最大值;
②当S取得最大值时,在抛物线上是否存在点R,使得以E,B,R,F为顶点的四边形是平行四边形?如果存在,求出点R的坐标;如果不存在,请说明理由.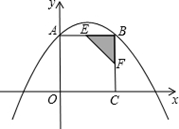
已知A、B两地相距300千米,甲、乙两车同时从A地出发,以各自的速度匀速往返两地,甲车先到达B地,停留1小时后按原路返回.设两车行驶的时间为x小时,离开A地的距离是y千米,如图是y与x的函数图象.
(1)计算甲车的速度为千米/时,乙车的速度为千米/时;
(2)几小时后两车相遇;
(3)在从开始出发到两车相遇的过程中,设两车之间的距离为S千米,乙车行驶的时间为t小时,求S与t之间的函数关系式.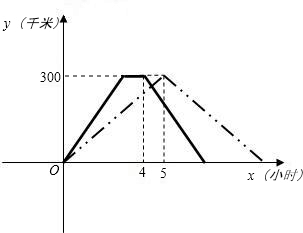
“初中生骑电动车上学”的现象越来越受到社会的关注,某校利用“十一”假期,随机抽查了本校若干名学生和部分家长对“初中生骑电动车上学”现象的看法,统计整理制作了如下的统计图,请回答下列问题:
(1)这次抽查的家长总人数是多少?
(2)请补全条形统计图和扇形统计图;
(3)从这次接受调查的学生中,随机抽查一个学生恰好抽到持“无所谓”态度的概率多少?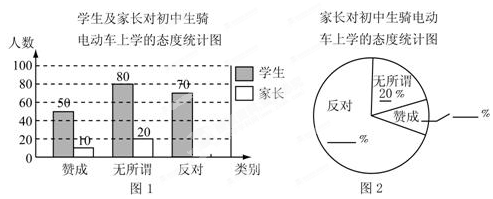
有两个可以自由转动的均匀转盘A,B都被分成了3等分,并在每一份内均标有数字,如图所示,规则如下:①分别转动转盘A,B;②两个转盘停止后观察两个指针所指份内的数字(若指针停在等分线上,那么重转一次,直到指针指向某一份内为止).
(1)请用树状图或列表法列出所有可能的结果;
(2)王磊和张浩想用这两个转盘做游戏,他们规定:若“两个指针所指的数字都是方程x2-5x+6=0的解”时,王磊得1分;若“两个指针所指的数字都不是方程x2-5x+6=0的解”时,张浩得3分,这个游戏公平吗?为什么?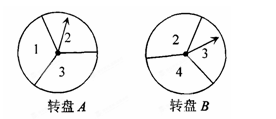
机器人“海宝”在某圆形区域表演“按指令行走”,如图所示,“海宝”从圆心O出发,先沿北偏西67.4°方向行走13米至点A处,再沿正南方向行走14米至点B处,最后沿正东方向行走至点C处,点B、C都在圆O上.
(1)求弦BC的长;
(2)求圆O的半径长.
(本题参考数据:sin 67.4° = ,cos 67.4°=
,cos 67.4°= ,tan 67.4° =
,tan 67.4° = )
)