选修4-1:几何证明选讲
已知 中,
中, ,D是
,D是 外接圆劣弧
外接圆劣弧 上的点(不与点A,C重合),延长BD至E.
上的点(不与点A,C重合),延长BD至E.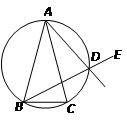
(1)求证:AD的延长线平分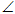 CDE;
CDE;
(2)若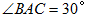 ,
, 中BC边上的高为2+
中BC边上的高为2+ ,求
,求 外接圆的面积.
外接圆的面积.
(本题12分)设函数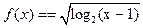 的定义域为A,集合
的定义域为A,集合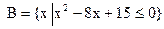 ,
,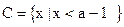 (1)求
(1)求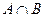 ;(2)若
;(2)若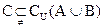 ,求
,求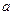 的取值范围。
的取值范围。
(本题12分)已知函数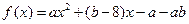 ,当
,当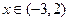 时,
时,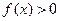 ;当
;当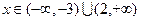 时,
时,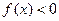 .(1)
.(1)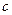 为何值时
为何值时 的解集为
的解集为 ;(2)求
;(2)求 在
在 内的值域.
内的值域.
(本题12分)已知函数 ,当
,当 时,
时, ;当
;当 时,
时,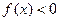 .(1)
.(1)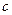 为何值时
为何值时 的解集为
的解集为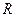 ;(2)求
;(2)求 在
在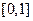 内的值域.
内的值域.
(本题12分)对于函数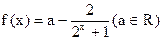 为奇函数(Ⅰ)求
为奇函数(Ⅰ)求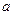 的值;(Ⅱ)用函数单调性定义及指数函数性质证明:
的值;(Ⅱ)用函数单调性定义及指数函数性质证明:  在
在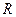 上是增函数。
上是增函数。
(本题12分)某一中校办工厂生产学生校服的固定成本为20000元,每多生产一件需要增加投入100元,已知总收益R(x)满足函数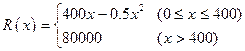 ,其中x是校服的月产量,问:(1)将利润表示为关于月产量x的函数
,其中x是校服的月产量,问:(1)将利润表示为关于月产量x的函数 .(2)当月产量为何值时,工厂所获利润最大?最大利润为多少元?(总收益=总成本+利润)
.(2)当月产量为何值时,工厂所获利润最大?最大利润为多少元?(总收益=总成本+利润)