在△ABC中,内角A、B、C对边的边长分别是a、b、c.已知c=2,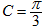 .
.
(1)若△ABC的面积等于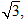 求a与b的值;
求a与b的值;
(2)若sinB=2sinA,求△ABC的面积.
已知复数 满足:
满足: 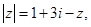 求
求 的值.
的值.
已知向量 =(
=( sin
sin ,1),
,1),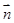 =(cos
=(cos ,cos2
,cos2 )
)
(1)若 ·
·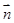 =1,求cos(
=1,求cos( -x)的值;
-x)的值;
(2)记f(x)= ·
·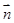 ,在△ABC中,角A,B,C的对边分别是a,b,c,且满足(2a-c)cosB=bcosC,求函数f(A)的取值范围.
,在△ABC中,角A,B,C的对边分别是a,b,c,且满足(2a-c)cosB=bcosC,求函数f(A)的取值范围.
在海岸A处,发现北偏东45°方向距A为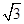 -1海里的B处有一艘走私船,在A处北偏西75°的方向,距A为2海里的C处的缉私船奉命以10
-1海里的B处有一艘走私船,在A处北偏西75°的方向,距A为2海里的C处的缉私船奉命以10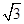 海里/小时的速度追截走私船.此时走私船正以10海里/小时的速度从B处向北偏东30°方向逃窜,问缉私船沿着什么方向能最快追上走私船?并求出所需要的时间.(注:
海里/小时的速度追截走私船.此时走私船正以10海里/小时的速度从B处向北偏东30°方向逃窜,问缉私船沿着什么方向能最快追上走私船?并求出所需要的时间.(注: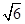 ≈2.449)
≈2.449)
在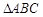 中,已知
中,已知
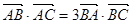
(1)求证: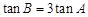
(2)若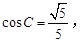 求A的值.
求A的值.
设函数 (其中
(其中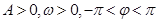 )在
)在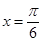 处取得最大值2,其图象与轴的相邻两个交点的距离为
处取得最大值2,其图象与轴的相邻两个交点的距离为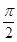
(I)求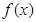 的解析式;
的解析式;
(II)求函数 的值域。
的值域。