在平面直角坐标系 中,已知圆
中,已知圆 经过
经过 ,
, 两点,且圆心在直线
两点,且圆心在直线 上.
上.
(1)求圆 的标准方程;
的标准方程;
(2)过圆 内一点
内一点 作两条相互垂直的弦
作两条相互垂直的弦 ,当
,当 时,求四边形
时,求四边形 的面积.
的面积.
(3)设直线 与圆
与圆 相交于
相交于 两点,
两点, ,且
,且 的面积为
的面积为 ,求直线
,求直线 的方程.
的方程.
已知线段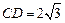 ,
,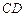 的中点为
的中点为 ,动点
,动点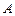 满足
满足 (
(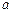 为正常数).
为正常数).
(1)建立适当的直角坐标系,求动点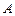 所在的曲线方程;
所在的曲线方程;
(2)若存在点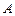 ,使
,使 ,试求
,试求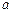 的取值范围;
的取值范围;
(3)若 ,动点
,动点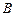 满足
满足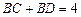 ,且
,且 ,试求
,试求 面积的最大值和最小值.
面积的最大值和最小值.
已知抛物线C: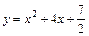 ,过C上一点M,且与M处的切线垂直的直线称为C在点M的法线.
,过C上一点M,且与M处的切线垂直的直线称为C在点M的法线.
(1)若C在点M的法线的斜率为 ,求点M的坐标(x0,y0);
,求点M的坐标(x0,y0);
(2)设P(-2,a)为C对称轴上的一点,在C上是否存在点,使得C在该点的法线通过点P?若有,求出这些点,以及C在这些点的法线方程;若没有,请说明理由.
如图,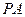 是圆
是圆 的切线,切点为
的切线,切点为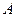 ,过
,过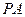 的中点
的中点 作割线交圆
作割线交圆 于
于 和
和 ,求证:
,求证: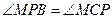 .
.
已知动点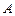 到两个定点
到两个定点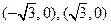 的距离的和等于4.
的距离的和等于4.
(1)求动点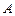 所在的曲线
所在的曲线 的方程;
的方程;
(2)若点 在曲线
在曲线 上,且
上,且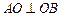 ,试求
,试求 面积的最大值和最小值.
面积的最大值和最小值.
已知函数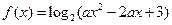
(1)当 时,求该函数的定义域和值域;
时,求该函数的定义域和值域;
(2)如果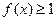 在区间
在区间 上恒成立,求实数
上恒成立,求实数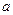 的取值范围.
的取值范围.