已知三个数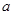 ,
,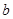 ,
,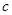 成等比数列,其公比为3,如果
成等比数列,其公比为3,如果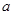 ,
,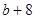 ,
,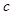 成等差数列,求这三个数.
成等差数列,求这三个数.
已知函数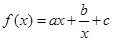 (
(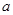 >0)的图象在点
>0)的图象在点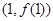 处的切线方程为
处的切线方程为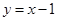 .
.
(1)用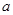 表示
表示 ;
;
(2)若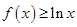 在
在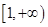 上恒成立,求
上恒成立,求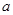 的取值范围;
的取值范围;
(3)证明:1+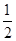 +
+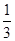 +…+
+…+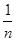 >
> +
+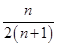
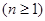 .
.
某汽车生产企业上年度生产一品牌汽车的投入成本为10万元/辆,出厂价为13万/辆,年销售量为5000辆.本年度为适应市场需求,计划提高产品档次,适当增加投入成本,若每辆车投入成本增加的比例为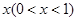 , 则出厂价相应提高的比例为
, 则出厂价相应提高的比例为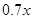 ,年销售量也适当增加.设年利润=(每辆车的出厂价-每辆车的投入成本)×年销售量
,年销售量也适当增加.设年利润=(每辆车的出厂价-每辆车的投入成本)×年销售量
(1) 若年销售量增加的比例为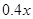 ,为使本年度的年利润比上年度有所增加,则投入成本增加的比例
,为使本年度的年利润比上年度有所增加,则投入成本增加的比例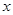 应在什么范围内?
应在什么范围内?
(2) 若本年度的销售量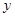 (辆)关于
(辆)关于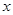 的函数为
的函数为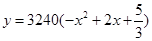 ,则当
,则当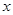 为何值时,本年度的年利润最大?最大利润为多少?
为何值时,本年度的年利润最大?最大利润为多少?
设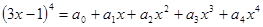 。
。
求:(1)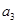
(2)求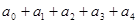 ;
;
(3)求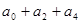 ;
;
(4)求各项二项式系数的和.
给定数字0、1、2、3、5、9每个数字最多用一次
(1)可能组成多少个四位数?
(2)可能组成多少个四位奇数?
(3)可能组成多少个自然数?