已知数列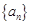 的前
的前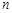 项和为
项和为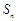 ,
,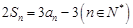 .
.
(1)求数列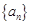 的通项公式;
的通项公式;
(2)若数列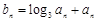 ,求数列
,求数列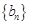 的的前
的的前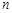 项和
项和 .
.
已知函数f(x)= 是定义在(-1,1)上的奇函数,且f(
是定义在(-1,1)上的奇函数,且f( )=
)= .
.
(1)试确定函数f(x)的解析式;(2)用定义证明f(x)在(-1,1)上是增函数;(3)解不等式f(t-1)+f(t)<0.
已知集合A =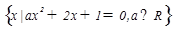 ,
,
(1)若 A,求a的值;(2)若A中有且只有一个元素,求a的值,并求出这个元素。
A,求a的值;(2)若A中有且只有一个元素,求a的值,并求出这个元素。
已知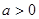 ,函数
,函数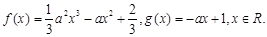
(1)当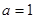 时,求函数
时,求函数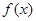 在点(1,
在点(1, )的切线方程;
)的切线方程;
(2)求函数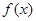 在[-1,1]的极值;
在[-1,1]的极值;
(3)若在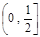 上至少存在一个实数x0,使
上至少存在一个实数x0,使 >g(xo)成立,求正实数
>g(xo)成立,求正实数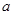 的取值范围。
的取值范围。
设椭圆  :
: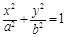 (
(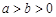 )的一个顶点为
)的一个顶点为 ,
,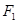 ,
, 分别是椭圆的左、右焦点,离心率
分别是椭圆的左、右焦点,离心率  ,过椭圆右焦点
,过椭圆右焦点  的直线
的直线  与椭圆
与椭圆 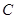 交于
交于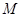 ,
, 两点.
两点.
(1)求椭圆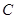 的方程;
的方程;
(2)是否存在直线  ,使得
,使得 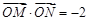 ,若存在,求出直线
,若存在,求出直线  的方程;若不存在,说明理由;
的方程;若不存在,说明理由;
在棱长为 的正方体
的正方体 中,
中, 是线段
是线段 的中点,
的中点,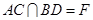 .
.
(1) 求证: ^
^ ;
;
(2) 求证: //平面
//平面 ;
;
(3) 求三棱锥 的表面积.
的表面积.