如图,已知矩形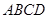 所在平面外一点
所在平面外一点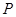 ,
,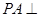 平面
平面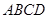 ,
,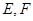 分别是
分别是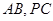 的中点,
的中点,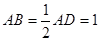 .
.
(1)求证: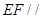 平面
平面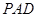 ;
;
(2)若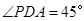 ,求直线
,求直线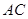 与平面
与平面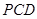 所成角的正弦值.
所成角的正弦值.
(本小题满分12分)已知 ,
, 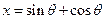 ,
,
(Ⅰ)把 表示为
表示为 的函数
的函数 并写出定义域;
并写出定义域;
(Ⅱ)求 的最值.
的最值.
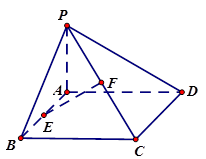
(本小题满分12分)已知三棱锥P—ABC中,PC⊥底面ABC,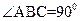 ,
, ,
,
二面角P-AB-C为 ,D、F分别为AC、PC的中点,DE⊥AP于E.
,D、F分别为AC、PC的中点,DE⊥AP于E.
(Ⅰ)求证:AP⊥平面BDE;
(Ⅱ)求直线EB与平面PAC所成的角。
(本小题满分12分)已知数列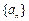 的首项为
的首项为 ,前
,前 项和为
项和为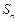 ,且对任意的
,且对任意的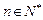 ,
,
当 时,
时, 总是
总是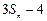 与
与 的等差中项.
的等差中项.
(Ⅰ)求数列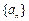 的通项公式;
的通项公式;
(Ⅱ)设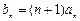 ,
, 是数列
是数列 的前
的前 项和,
项和,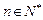 ,求
,求 .
.
(本小题满分12分)在一个选拔项目中,每个选手都需要进行4轮考核,每轮设有一个问
题,能正确回答者进入下一轮考核,否则被淘汰。已知某选手能正确回答第一、二、三、
四轮问题的概率分别为 、
、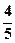 、
、 、
、 ,且各轮问题能否正确回答互不影响。
,且各轮问题能否正确回答互不影响。
(Ⅰ)求该选手进入第三轮才被淘汰的概率;
(Ⅱ)求该选手至多进入第三轮考核的概率;
(本小题满分10分)已知向量 ,
, 。
。
(Ⅰ)若 ,求
,求 的值;
的值;
(Ⅱ)设 ,求
,求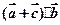 的取值范围.
的取值范围.