如图,在长为10千米的河流OC的一侧有一条观光带,观光带的前一部分为曲线段OAB,设曲线段OAB为函数 ,
, (单位:千米)的图象,且图象的最高点为
(单位:千米)的图象,且图象的最高点为 ;观光带的后一部分为线段BC.
;观光带的后一部分为线段BC.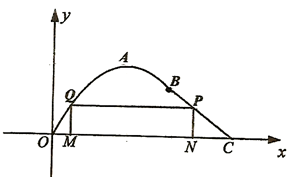
(1)求函数为曲线段OABC的函数 的解析式;
的解析式;
(2)若计划在河流OC和观光带OABC之间新建一个如图所示的矩形绿化带MNPQ,绿化带由线段MQ,QP,PN构成,其中点P在线段BC上.当OM长为多少时,绿化带的总长度最长?
已知数列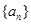 满足
满足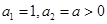 ,数列
,数列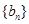 满足
满足
(1)若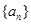 为等比数列,求
为等比数列,求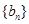 的前n项的和
的前n项的和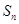 ;
;
(2)若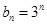 ,求数列
,求数列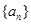 的通项公式;
的通项公式;
(3)若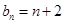 ,求证:
,求证: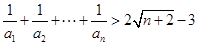
(本小题满分16分)已知椭圆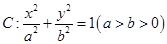 的离心率为
的离心率为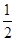 ,且过点
,且过点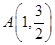 .
.
(1)求椭圆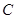 的方程;
的方程;
(2)若点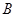 在椭圆上,点
在椭圆上,点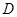 在
在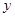 轴上,且
轴上,且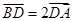 ,求直线
,求直线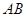 方程.
方程.
(本小题满分14分)小张于年初支出50万元购买一辆大货车,第一年因缴纳各种费用需支出6万元,从第二年起,每年都比上一年增加支出2万元,假定该车每年的运输收入均为25万元.小张在该车运输累计收入超过总支出后,考虑将大货车作为二手车出售,若该车在第x年年底出售,其销售收入为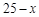 万元(国家规定大货车的报废年限为10年).
万元(国家规定大货车的报废年限为10年).
(1)大货车运输到第几年年底,该车运输累计收入超过总支出?
(2)在第几年年底将大货车出售,能使小张获得的年平均利润最大?(利润=累计收入+销售收入-总支出)
(本小题满分14分)已知三棱锥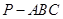 中,
中,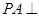 平面
平面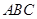 ,
,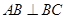 ,
,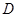 为
为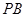 中点,
中点,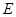 为
为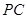 的中点,
的中点,
(1)求证: 平面
平面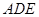 ;
;
(2)求证:平面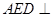 平面
平面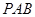 .
.
(本小题满分14分)已知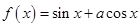 ,
,
(1)若 ,求
,求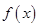 的最大值及对应的x的值.
的最大值及对应的x的值.
(2)若 ,
, 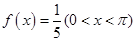 ,求tanx的值.
,求tanx的值.