在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个球被取出的可能性相等.
(1)求取出的两个球上标号为相同数字的概率;
(2)求取出的两个球上标号之积能被3整除的概率.
(本题满分12分),
如图,菱形ABCD所在平面与矩形ACEF所在平面互相垂直,已知BD= AF,且点M是线段EF的中点.
AF,且点M是线段EF的中点.
(1)求证:AM∥平面BDE;
(2)求平面DEF与平面BEF所成的角.
(本小题满分12分)
已知向量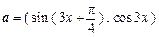 ,函数
,函数 .求:
.求:
(1)函数 的最小值;
的最小值;
(2)函数 的单调递
的单调递 增区间.
增区间.
已知函数 将
将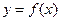 的图象向右平移两个单位,得到
的图象向右平移两个单位,得到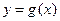 的图象.
的图象.
(1)求函数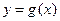 的解析式;
的解析式;
(2) 若函数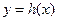 与函数
与函数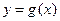 的图象关于直线
的图象关于直线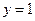 对称,求函数
对称,求函数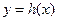 的解析式;
的解析式;
(3)设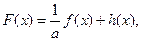 已知
已知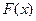 的最小值是
的最小值是 ,且
,且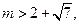 求实数
求实数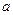 的取值范围.
的取值范围.
数列{an}的前n项和记为Sn,
(1)求{an}的通项公式
(2)等差数列{bn}的中, ,求数列
,求数列 的前n项和为Tn
的前n项和为Tn
用长为90cm,宽为48cm的长方形铁皮做一个无盖的容器,先在四角分别截去一个小正方形,然后把四边翻折900角,再焊接而成,问该容器的高为多少时,容器的容积最大?最大的容积是多少?