在北京2008年第29届奥运会前夕，某超市在销售中发现：奥运会吉祥物“福娃”平均每天可售出20套，每套盈利40元。为了迎接奥运会，商场决定采取适当的降价措施，扩大销售量，增加盈利，尽快减少库存。经市场调查发现：如果每套降价1元，那么平均每天就可多售出2套．
（1）要想平均每天在销售吉祥物上盈利1200元，那么每套应降价多少？
（2）每套吉祥物降价多少元时，才能使每天的利润最大，最大利润为多少元？
已知:r如图，在梯形ABCD中，AD∥BC，∠BCD=90°.对角线AC、BD相交于点E。且AC⊥BD。（1）求证：CD²=BC·AD；（2）点F是边BC上一点，连接AF，与BD相交于点G，如果∠BAF=∠DBF，求证：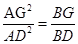
。
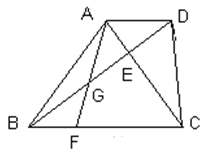
如图，已知某船向正东方向航行，在点A处测得某岛C在其北偏东60°方向上，前进8海里到达点B处，测得岛C在其北偏东30方向上，已知岛C周围6海里内有一暗礁，问：如果该船继续向东航行，有无触礁危险？请说明你的理由。
已知，如图，在平行四边形ABCD中，E、F分别是边BC、CD上的点，且EF∥BD，AE、AF分别交BD于点G和点H，BD=12，EF=8。求：（1）
的值。（2）线段GH的长。
如图，已知在△ABC中，点D、E分别在边AB和AC上，DE∥BC,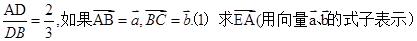
；(2)求作向量
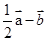（不要求写作法，但要指出所作图中表示结论的向量）。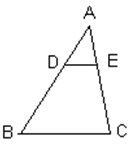
如图，已知抛物线y=x2-1与x轴交于A、B两点，与y轴交于点C．
（1）求A、B、C三点的坐标．
（2）过点A作AP∥CB交抛物线于点P，求四边形ACBP的面积．
（3）在
轴上方的抛物线上是否存在一点M，过M作MG
轴于点G，使以A、M、G三点为顶点的三角形与
PCA相似．若存在，请求出M点的坐标；否则，请说明理由．